Antes de conocer cómo calcular las métricas de evaluación de modelos de clasificación, debemos atender un concepto de uso común en la labor del científico de datos: los datos desbalanceados.
Esta propiedad en la estructura de los datos, que puede llegar a ser problemática, será explorada aquí de manera breve pero detallada, de forma que comprenderemos de qué se trata, qué problemas plantea, y cómo podemos detectarlo.

Estadística descriptiva

Fundamentos de conjuntos de datos y datos etiquetados

Algún acompañamiento

Datos desbalanceados, definición y ejemplos

Los conjuntos de datos no son perfectos. Generalmente, contienen irregularidades que son tratadas principalmente en la etapa de preprocesamiento. Entre estos desperfectos, se pueden tener estructuras en las que los datos no se encuentren distribuidos de manera equilibrada, afectando el entrenamiento de modelos de aprendizaje de máquinas; a esto se le conoce como datos desbalanceados.
De forma más concisa, los datos desbalanceados son una característica de un conjunto de datos en el que la distribución de una o más variables de interés está sesgada, es decir, ciertos valores, clases o rangos de datos están representados de manera desigual en comparación con otros.
En el contexto del aprendizaje supervisado, en lo que se refiere datos etiquetados en los que se han definido variables de entrada y variables de salida, un desbalance de este tipo no permitiría el entrenamiento óptimo de un modelo de machine learning.
¿Aún no captas por completo el concepto?, lo ilustraremos con un ejemplo para tareas tanto de clasificación como de regresión.
Datos desbalanceados para entrenar modelos de clasificación
Recordemos que en conjuntos de datos que se utilizan para entrenar un modelo clasificador, se etiquetan los datos de forma que cada ejemplo de entrenamiento pertenece a alguna clase particular. Un caso de datos perfectamente balanceados es el siguiente:

En la Tabla 3.6.1.1 se puede observar cómo se tienen 5 valores asignados a la clase 1, y 5 valores asignados a la clase 0 (la mitad). Esto indica que tenemos los datos balanceados, ya que se tiene una cantidad igual de datos pertenecientes a cada clase.
Si trasladamos esto al caso que trabajamos con la regresión logística, se tendrían la mitad de datos asignados a la clase Black Metal, y el otro a la clase Reggaeton (y los valores de la variable de entrada corresponderían a la bailabilidad).
Podemos utilizar otro ejemplo como el de detección de fraudes: la clase 1 indica que una transacción es fraudulenta, mientras que la clase 0 indica que no lo es, y las variables a considerar pueden ser datos demográficos o de comportamiento del usuario.
Aquí lo que importa realmente es la porción que existe etiquetada para cada clase: si se tuviera un millón de datos, estos estarían perfectamente balanceados si la mitad estuvieran etiquetados a una clase y la mitad restante a la otra clase (500 mil y 500 mil, respectivamente).

En el caso de haber más clases se estaría buscando igualdad de proporción de cada una de estas en el conjunto de datos; por ejemplo, en un escenario ideal, un conjunto de datos etiquetado con cuatro clases tendría que tener, idealmente, la siguiente distribución:
- Clase 1: 25%
- Clase 2: 25%
- Clase 3: 25%
- Clase 4: 25%
O, en un conjunto con tres clases, se esperaría aproximadamente esto:
- Clase 1: 33.33%
- Clase 2: 33.33%
- Clase 3: 33.33%

No sucede nada, lo que se busca es tener datos relativamente balanceados, de forma que el entrenamiento del modelo no se termine sesgando. Es casi imposible que hallemos datos que, naturalmente, cuenten con balances perfectos, solo debemos procurar ser conscientes de las distribuciones de estos y sus posibles efectos durante la etapa de entrenamiento.
Vayamos con un ejemplo de lo que implica esto. Si tenemos la mayoría de los ejemplos de entrenamiento etiquetados para solo una clase, entonces el modelo aprenderá a predecir esta clase con efectividad, pero no podrá realizar inferencias precisas sobre la clase o clases restantes.
En la Tabla 3.6.1.2 se puede observar el mismo ejemplo que hemos visualizado con anterioridad, pero con las clases desbalanceadas:
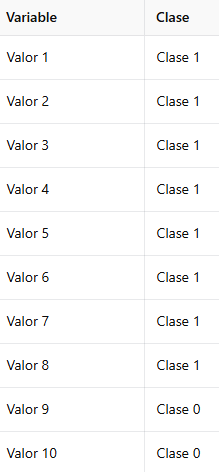
En esta última tabla, es notorio cómo la clase 0 contiene menos datos asignados que la clase 1, de forma que la proporción queda como sigue:
- Clase 1: 80%
- Clase 0: 20%
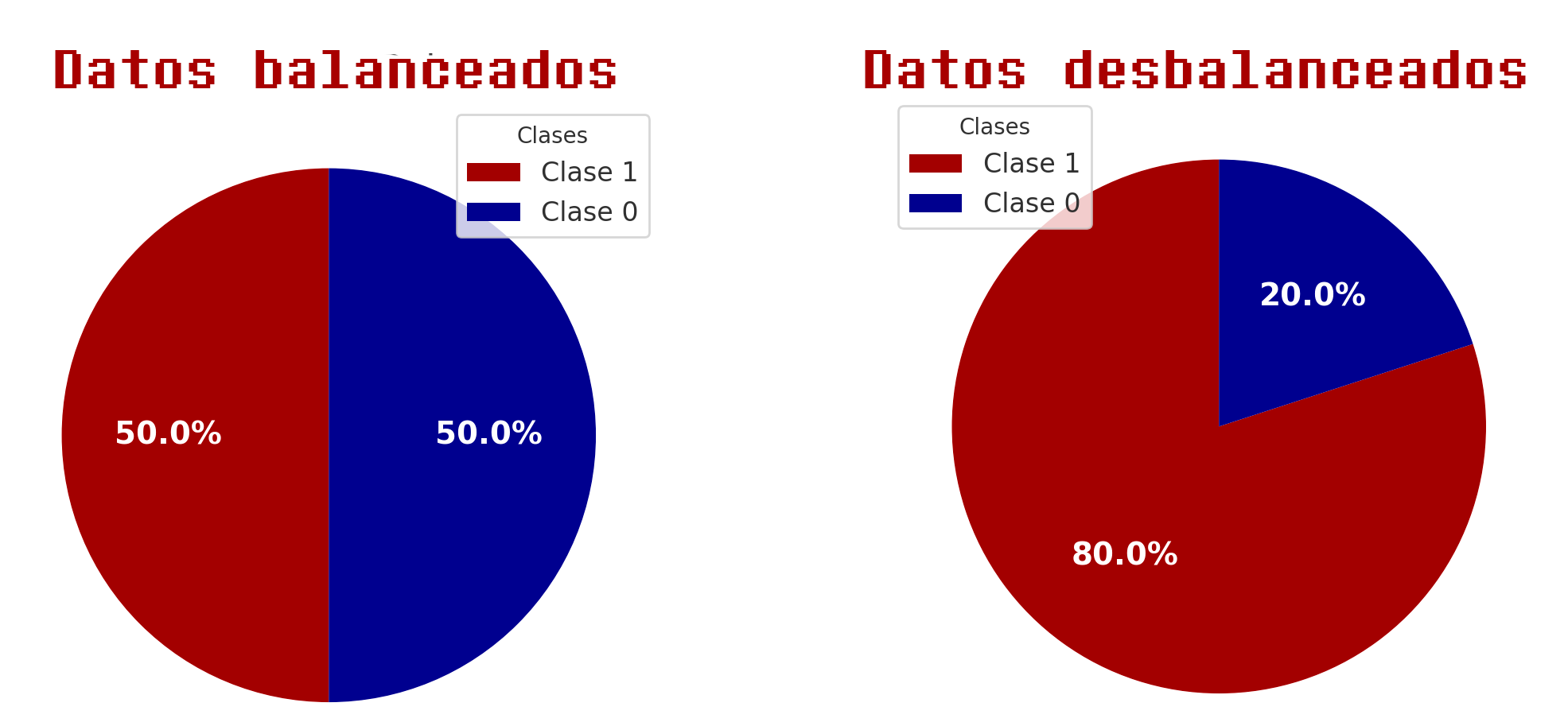
Una distribución de este tipo impide un modelado efectivo para la predicción de ambas clases. Una excelente manera de percibir un desbalanceo en un conjunto de datos es mediante representaciones gráficas:

Vamos hacia allá.
Métricas y reglas para determinar si los datos están desbalanceados
Existen diversos métodos para determinar si un conjunto de datos para tareas de clasificación está desbalanceado, a continuación describiremos algunos de los más utilizados.
Ratio de desequilibrio
Una medida sencilla para identificar desbalance de clases en un conjunto de datos es calcular la proporción de asignación de las clases. Para esto se puede utilizar la medida de ratio de desequilibrio (imbalanced ratio):
\text{Imbalanced Ratio (IR)} = \frac{\text{Tamaño de la clase mayoritaria}}{\text{Tamaño de la clase minoritaria}}, \tag{3.68.1}
donde la clase mayoritaria es aquella que acapara la mayor cantidad de datos.
El criterio convencionalmente aceptado para interpretar esta métrica es que un conjunto de datos con un valor de ratio de desequilibrio mayor a 2 (IR\ge2) puede considerarse desbalanceado, tomando en cuenta la naturaleza de los datos.
Si utilizamos el ejemplo de la Tabla 3.6.1.2, el cálculo del IR es:
\text{IR} = \frac{\text{8}}{\text{2}}=4 \tag{3.68.2}
Este resultado implicaría un gran desbalanceo, ya que un valor de (IR=1) indica un equilibrio perfecto entre las clases (\frac{50}{50}).
Porcentaje de la clase minoritaria (Minority Class Percentage)
Este porcentaje evalúa qué proporción del total representa la clase minoritaria (aquella que aparece con menos frecuencia). Si la clase minoritaria representa menos del 30% de los datos, es probable que haya desbalance. Volviendo al ejemplo anterior:
- Clase 1: 80%
- Clase 0: 20%
Aquí, la clase minoritaria es menos del 30%, lo cual indica un posible desbalance.
Existen otras variadas formas de determinar un desequilibrio significativo entre clases en un conjunto de datos:
- Utilizar gráficas como las que se visualizaron en la Figura 3.6.1.1.
- Utilizar métricas basadas en el desempeño del modelo, las cuales veremos en nuestra próxima exploración.
- Para conjuntos de datos con más de dos clases (multiclase), se puede consultar Measuring the Class-imbalance Extent of Multi-class Problems de Hernández y Lozano.
Con esto debería quedar claro cómo lucen los datos desbalanceados. Recuerda que siempre hay que evaluar el impacto de esto conforme al contexto de los datos y diferentes métricas para la evaluación del conjunto de datos y del modelo entrenado mediante su ingesta.
Datos desbalanceados en conjuntos de datos para entrenar modelos de regresión
Hemos visto cómo lucen los conjuntos de datos con clases desbalanceadas en conjuntos etiquetados con categorías cuyo destino es el entrenamiento de modelos de clasificación. Revisemos cómo se puede dar esto en conjuntos de datos con objetivos de entrenamiento de modelos de regresión.
En un conjunto de datos destinado a una tarea de regresión, los datos desbalanceados se refieren a una distribución no uniforme de la variable objetivo (variable dependiente o salidas) en el rango de valores que esta puede tomar. Aunque el concepto de clases no aplica como en la clasificación, el desbalance puede manifestarse en los siguientes casos:
Concentración de valores en pocos rangos
En un conjunto de datos desbalanceado la mayoría de los valores de las salidas pueden estar concentrados en un rango específico, dejando a los rangos restantes con pocos ejemplos de entrenamiento.
Recordemos el ejemplo de los alumnos y sus calificaciones respecto a horas de estudio que atendimos en la lección sobre la regresión lineal. Podríamos tener un conjunto de datos como este:
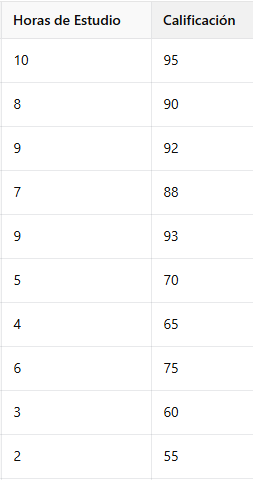
En la Tabla 3.6.1.3 puedes notar cómo la mayoría de las calificaciones son altas (mayores a 85). Esto ocasionaría que un modelo entrenado con estos datos no sea capaz de predecir correctamente calificaciones con valores más bajos. Un histograma de estos datos con los rangos mencionados se puede observar en la Figura 3.6.1.2:
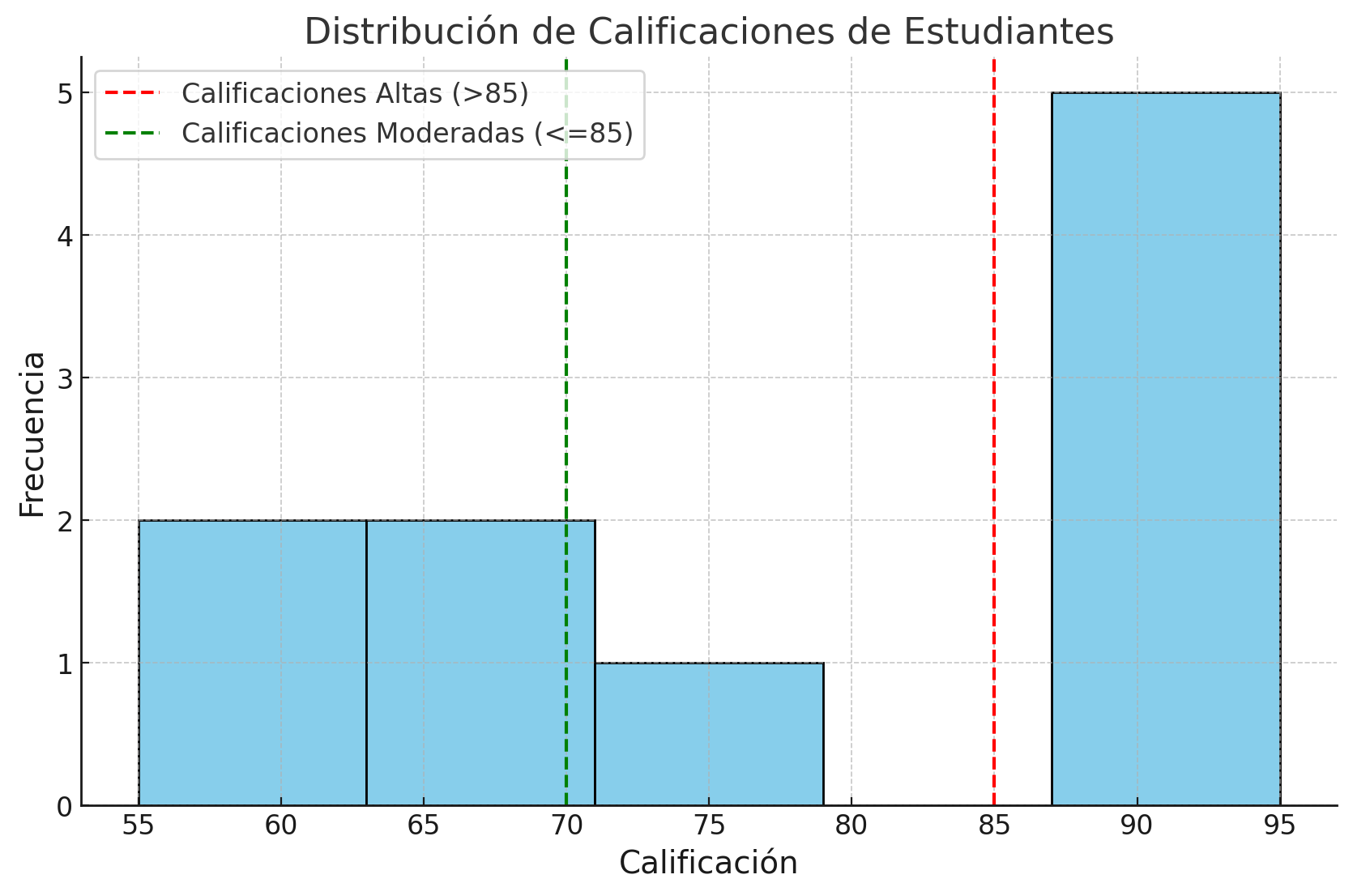
Presencia de valores atípicos (outliers)
Se pueden desbalancear los datos si se cuenta con valores atípicos en la variable objetivo, es decir, que están muy alejados del comportamiento de la mayoría de los datos. Esto ya lo hemos visto en nuestras actividades entrenando modelos, y hemos trabajado en deshacernos de este tipo de valores mediante diferentes métodos matemáticos.
Un ejemplo de esto luciría como se muestra en la Tabla 3.6.1.4:
Para discernirlo mejor, observemos la siguiente gráfica:
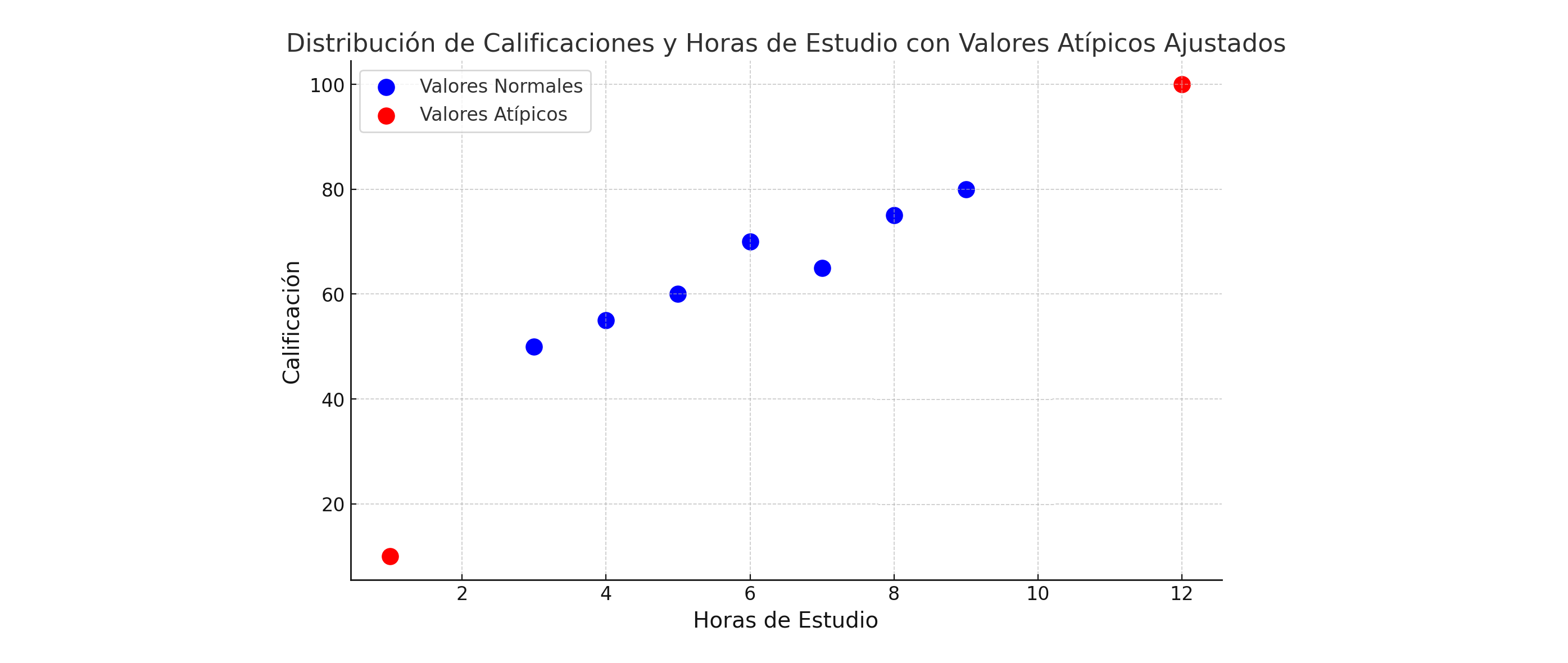
La aparición de este tipo de observaciones puede ocasionar sesgos en el rendimiento del modelo entrenado.
Sesgo en la Distribución
Otro tipo de desequilibrio en los datos se da cuando las entradas presentan una distribución sesgada, la cual es generada por valores que no se distribuyen de forma normal o simétrica.
En la Figura 3.6.1.5 se puede consultar cómo luce una gráfica de datos con una distribución aproximadamente normal, donde los valores caen alrededor de la media y la mediana, y también se aprecia una distribución asimétrica, donde la mayoría de los valores de calificaciones son altos, provocando una <<cola>> negativa, y un conglomerado en los valores positivos, generando un sesgo en los rangos de los valores.
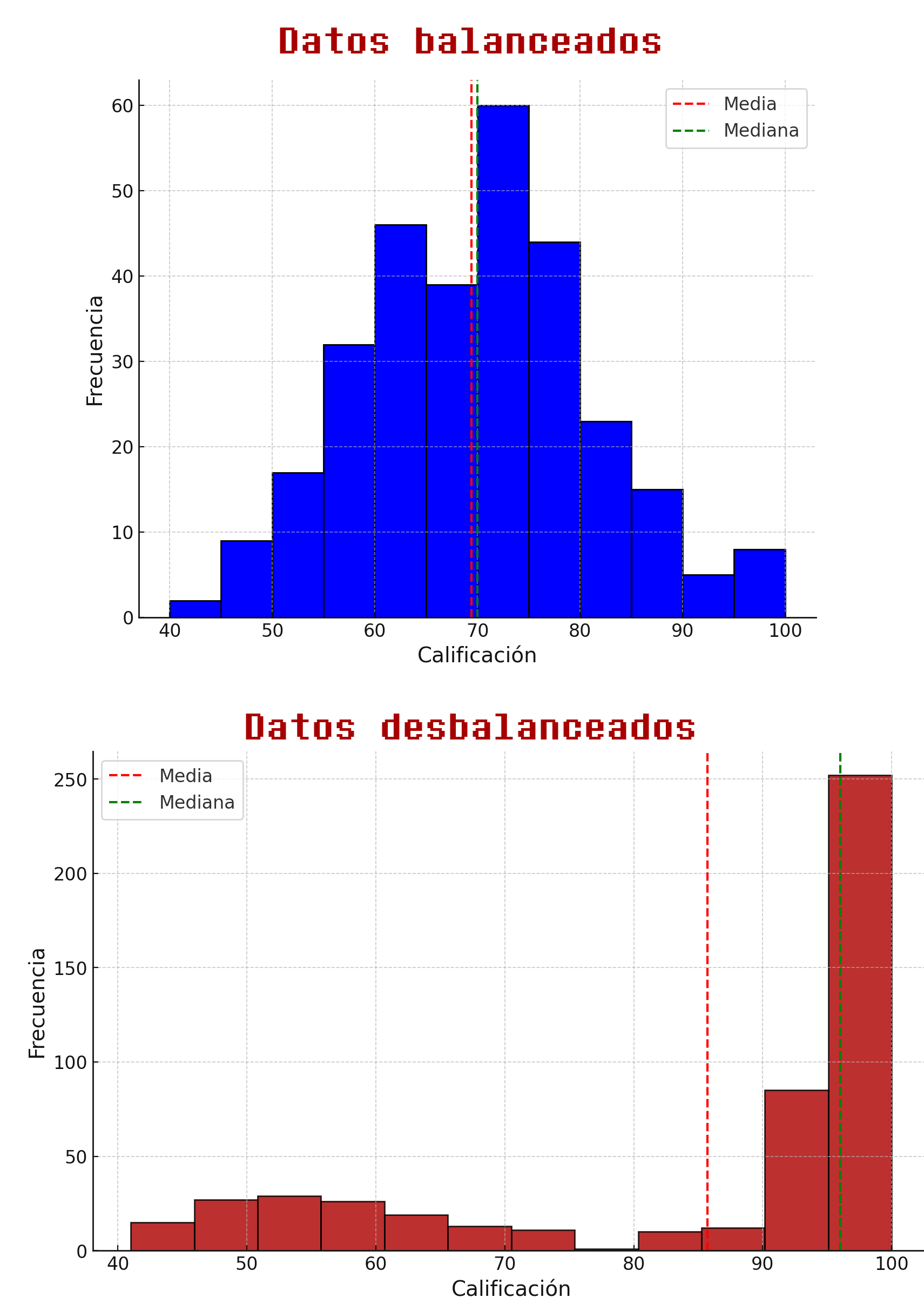
Cómo detectar datos desbalanceados para entrenamiento de modelos de regresión
Para hallar indicios de un conjunto de datos desequilibrado, podemos utilizar los siguientes métodos:
Coeficiente de asimetría
El coeficiente de asimetría (skewness) es una medida que indica si la distribución de los datos está sesgada hacia la izquierda (sesgo negativo) o hacia la derecha (sesgo positivo). Se calcula como sigue:
\text{Coeficiente de asimetría} = \frac{ \frac{1}{N} \sum_{i=1}^{N} (x_i - \bar{x})^3 }{ \left( \frac{1}{N} \sum_{i=1}^{N} (x_i - \bar{x})^2 \right)^{\frac{3}{2}} }, \tag{3.68.3}
donde N es la cantidad total de observaciones/datos, x_i es la i-ésima observación, y \bar{x} es la media de las observaciones.
El valor resultante se interpreta de la siguiente manera:
- Coeficiente de asimetría (Skewness) ≈ 0 → Distribución simétrica.
- Coeficiente de asimetría (Skewness) > 0 → Sesgo positivo (cola a la derecha).
- Coeficiente de asimetría (Skewness) < 0 → Sesgo negativo (cola a la izquierda).
Curtosis (kurtosis)
La curtosis mide cuánto peso tienen las colas de la distribución en comparación con una distribución normal. Se calcula:
\text{Curtosis} = \frac{ \frac{1}{N} \sum_{i=1}^{N} (x_i - \bar{x})^4 }{ \left( \frac{1}{N} \sum_{i=1}^{N} (x_i - \bar{x})^2 \right)^{2} }, \tag{3.68.4}
donde, de igual manera, N es la cantidad total de datos, x_i es la i-ésima observación, y \bar{x} es la media de las observaciones.
Esta medida se interpreta de la siguiente forma:
- Curtosis ≈ 3 → Distribución normal (Mesocúrtica).
- Curtosis > 3 → Colas más pesadas (Leptocúrtica, más valores extremos).
- Curtosis < 3 → Colas más ligeras (Platicúrtica, valores concentrados en el centro).
Coeficiente de variación
El Coeficiente de Variación (CV) es una métrica que indica altas variaciones en los datos, lo cual puede señalar posibles apariciones de datos atípicos, desbalanceando la distribución de estos.
Este se calcula como se muestra a continuación:
CV = \frac{\sigma}{\bar{x}}, \tag{3.68.5}
donde \sigma es la desviación estándar de los datos, y \bar{x} su promedio.
Se interpreta como sigue:
- CV ≈ 0 → Poca variabilidad (valores muy similares entre sí).
- CV alto (>0.5) → Alta dispersión (datos desbalanceados).
- CV muy alto (>1) → Datos extremadamente dispersos.
Además de estas medidas, se pueden utilizar las siguientes herramientas:
- Gráficas como las que hemos mostrado antes, donde se puedan visualizar diferencias significativas en la distribución de los datos.
- Técnicas para identificación de valores atípicos como el rango intercuartílico o isolation forest.
- Métricas de evaluación de modelos de regresión.
- Comparación entre la media y la mediana de las observaciones.


¿Podemos ponerlo en práctica? Sí, pero no creo que sea necesario. Estas métricas son relativamente sencillas de calcular, y vamos a ver datos desbalanceados sobre otras prácticas en las que usaremos conjuntos de datos para entrenar modelos. Por el momento, lo dejaremos así, tengan paciencia, esos datos desbalanceados llegarán eventualmente.

Eso es un tema que puede llegar a ser demasiado extenso, veremos estos métodos más adelante, cuando abarquemos tópicos avanzados y especializados de ciencia de datos.


