Como ya hemos aprendimos durante la introducción a las funciones de pérdida, el fin de estas funciones es realizar mediciones sobre qué tan cercanos a los datos reales son los cálculos realizados por un modelo entrenado con un algoritmo de aprendizaje de máquinas.
Cuando se trata de este tema, lo más convencional es iniciar su estudio utilizando como referencia las funciones de costo para algoritmos de regresión, como es el caso del error cuadrático medio (MSE). Sin embargo, es importante conocer cómo opera una función de pérdida para algoritmos de clasificación, para lo cual invocaremos y estudiaremos la función de error utilizada para la optimización de parámetros en la regresión logística y otros algoritmos de modelos de clasificación: la función de entropía cruzada binaria.

Inventario recomendado

Matemáticas
Álgebra y funciones.



Algún acompañamiento

Función de pérdida logística

Una función de pérdida que se puede utilizar para la evaluación de modelos de regresión logística, y en general de diversos modelos de clasificación de dos clases, es la función de entropía cruzada binaria (Cross-Entropy), también conocida como función de pérdida logística (Log-Loss). Su objetivo es determinar la cercanía de los cálculos de probabilidad dados por un modelo clasificador respecto a los valores del terreno real (aquellos pertenecientes al conjunto de datos recolectados). Es decir, determina qué tan bien realiza clasificaciones el modelo ajustado durante la etapa de entrenamiento.

La función de pérdida logística opera de forma similar a las funciones de costo de modelos de regresión que vimos anteriormente, pero con unas pequeñas diferencias que examinaremos a continuación.
Funcionamiento de la Entropía Cruzada Binaria
La manera en la que se determinan las pérdidas o errores en la función de entropía cruzada es mediante la determinación de qué tan lejanas se encuentran las probabilidades calculadas para determinadas clases.
Para esto debemos recordar que las salidas de un modelo clasificador como la función logística son probabilidades condicionales que nos dicen lo siguiente: ¿cuál es la probabilidad de que un dato de entrada pertenezca a una clase específica?

Al obtener estas probabilidades con el modelo ajustado, la función de pérdida logística obtiene las diferencias entre las probabilidades y las clases binarias (1 y 0).
Lo desarrollaremos en un ejemplo para comprenderlo mejor.
Ejemplo de función de pérdida logística
Para ilustrar el cálculo de los errores en un modelo clasificador, utilizaremos un ejemplo parecido al que trabajamos para abordar la regresión lineal, en el que trabajamos con un conjunto de datos de horas de estudio y calificaciones obtenidas.
Haremos algo muy similar, pero tornando el enfoque de un problema de regresión a uno de clasificación.
El objetivo será el siguiente: determinar si un alumno logra pasar o no un examen de acuerdo con sus horas de estudio.
Supongamos que la siguiente tabla es parte de nuestros datos:
| Horas de estudio (x) | ¿Aprobó el examen? (y) |
| 1 | 0 |
| 2.2 | 0 |
| 3.5 | 0 |
| 4 | 1 |
| 5.5 | 1 |
| 6 | 1 |
En los datos mostrados en la tabla se observa cómo para diferentes cantidades de horas de estudio dedicadas se aprueba o no el examen, lo cual genera dos clases, donde 0 significa que el estudiante no pasó el examen, y 1 significa que sí lo aprobó.
La relación entre las dos clases (variable dependiente) y las horas de estudio (variable independiente) la modelaremos realizando una regresión logística sobre la información dada.
Supongamos que hemos entrenado el modelo, y realizamos predicciones para cada dato mostrado en la tabla. Para obtener la pérdida total se realizan operaciones de comparación entre las salidas y observaciones del terreno real y las probabilidades calculadas. Estos cálculos los veremos de forma mucho más detallada en la sección de matemáticas, por el momento, la Figura 3.5.1, la cual es una versión ligeramente modificada de la Figura 3.4.1 perteneciente a nuestro último recorrido, ilustra el proceso de forma simplificada:
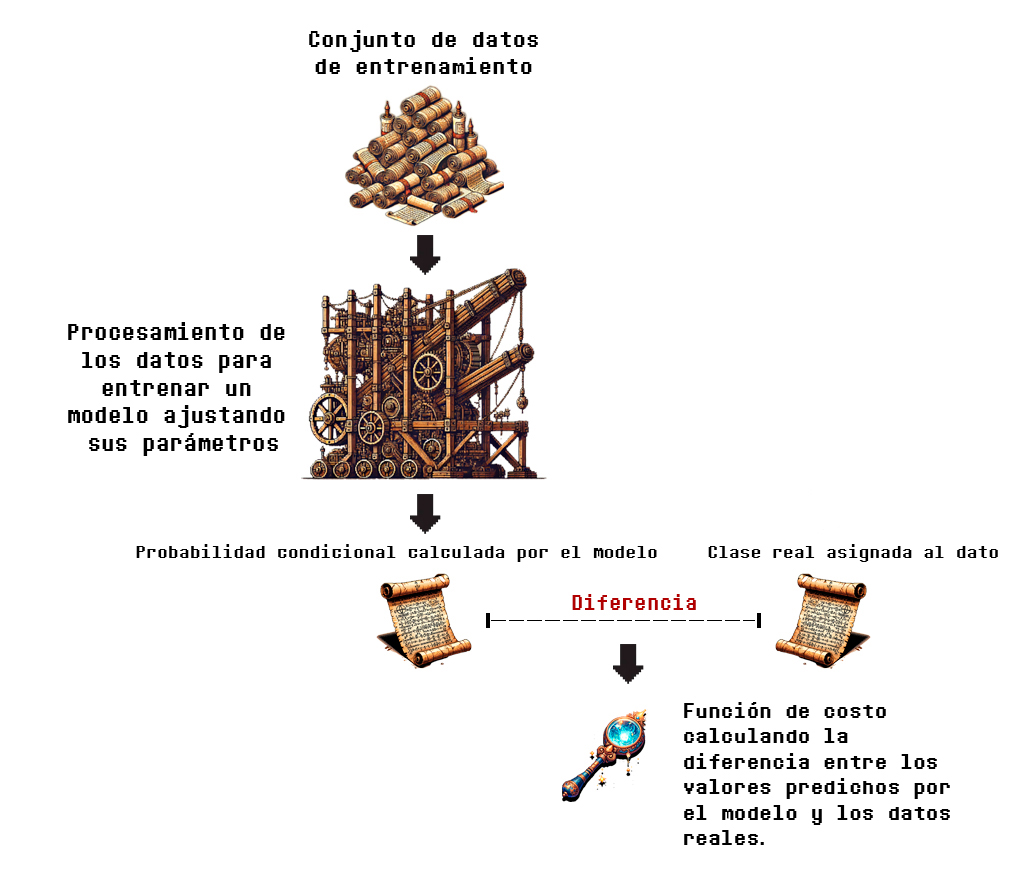
Como se puede observar, a diferencia de la función de pérdida que utilizamos para una regresión lineal, en este caso se obtienen las diferencias entre las probabilidades calculadas por el modelo (que están en el rango de 0 a 1) y las clases binarias (que, como sabemos, son 0 o 1).
Al final, estas diferencias se agregan y se obtiene un promedio (la pérdida total).
El cálculo de estos costos o pérdidas depende del uso de una fórmula que no se explicará aquí. Esta genera un número que expresa las diferencias entre las probabilidades calculadas por el modelo, y las etiquetas del terreno real, pero estas diferencias no se calculan directamente, son reexpresadas mediante un proceso matemático que se aprenderá en el siguiente apartado.
Por el momento, ilustraremos los pasos para la obtención de pérdida total logística en 4 puntos.
1. Primero, necesitamos calcular las pérdidas individuales utilizando la función de pérdida logística. Esta es la fórmula de la que te he hablado. Supondremos que hemos obtenido las pérdidas asociadas y las organizamos en una columna nueva:
| Horas de estudio (x) | ¿Aprobó el examen? (y) | Pérdida calculada |
| 1 | 0 | 0.311 |
| 2.2 | 0 | 0.798 |
| 3.5 | 0 | 1.70 |
| 4 | 1 | 0.127 |
| 5.5 | 1 | 0.029 |
| 6 | 1 | 0.018 |
2. Ahora, obtenemos la suma de estas pérdidas:
Suma de las pérdidas individuales: 2.987
3. Y, por último, calculamos el promedio:
Pérdida total: 2.987/6=0.49

El criterio a seguir para interpretar el resultado de la función de pérdida logística es el mismo que el que se tiene para la función de MSE:
- Valor de pérdida cercano a 0: Un valor bajo de pérdida logística indica que el modelo está haciendo buenas predicciones, es decir, las probabilidades predichas están cerca de las etiquetas reales.
- Valor de pérdida cercano a 1: Un valor alto de log-loss (pérdida logística) indica que el modelo está haciendo predicciones deficientes: las probabilidades predichas están lejos de las etiquetas reales.
Al haber obtenido un valor de pérdida de 0.49 en un conjunto con valores de entrada que van desde 1 a 6, podemos concluir que el modelo ajustado es eficiente al realizar las inferencias de clasificación para las que fue entrenado.
Definición matemática de la función de entropía cruzada binaria

Como vimos en la sección de matemáticas de la regresión logística, esta función modela la probabilidad de que una entrada x_n pertenezca a una clase particular y_n \in {0, 1} . La función de probabilidad para y_n = 1 dada una entrada x_n y los parámetros \theta está dada por:
\begin{aligned} \sigma(x) = p(y_n = 1 | x_n, \theta) = \frac{1}{1 + e^{-(\theta_0 + \sum_{i=1}^D \theta_i x_n^i)}}, \tag{3.28} \end{aligned}Donde \sigma(x) es la función sigmoide.
Definición (3.11) Función de entropía cruzada binaria. Sea \mathcal{D} = \lbrace (x_{1},y_{1}),…,(x_{N},y_{N})\rbrace un conjunto de N datos etiquetados, y \sigma(x) una función sigmoide como la definida en la Ecuación (3.28) que pretende mapear los valores de cada entrada x_n a su respectiva salida y_n, la función de pérdida de entropía cruzada es una función que mapea un conjunto de valores de ejemplos de entrenamiento a un número real, y está definida como sigue:
\begin{aligned} L(\mathcal{Y}, \mathcal{\hat{Y}})) = \frac{1}{N} \sum_{n=1}^N l(y_n, \sigma(x_n)) \end{aligned}, \tag{3.44}donde \mathcal{\hat{Y}} es el conjunto de todas las predicciones realizadas con el modelo \sigma(x) , y l es la función de pérdidas individuales definida como sigue:
\begin{aligned} l(y, \sigma(x)) = -[y \log(\sigma(x)) + (1 - y) \log(1 - \sigma(x))] \end{aligned}, \tag{3.45}la cual obtiene las diferencias entre las probabilidades predichas y sus clases correspondientes en el conjunto de datos.

Te doy un momento para pensarlo 👀
De acuerdo con la estructura de funciones de pérdida revisada en la anterior exploración, se pueden identificar los siguientes componentes:
- Agregador de pérdidas: \frac{1}{N} \sum_{i=1}^N
- Función de pérdidas individuales: -[y \log(\sigma(x)) + (1 - y) \log(1 - \sigma(x))]

A continuación, desarrollaremos con detalle cómo se llega a la forma final de esta función, y qué operaciones definen su utilidad.
Fundamentos matemáticos de la función de pérdida de la regresión logística
Volveremos a invocar (una vez más) la expresión (3.28), la cual es el modelo resultante de la regresión logística, y que nos arroja el cálculo de la probabilidad de que un dato de entrada x_n parametrizado por \theta pertenezca a la clase y_n = 1 :
\begin{equation} p(y_n = 1 | x_n, \theta) = \sigma(x_n) = \frac{1}{1 + e^{-(\theta_0 + \sum_{i=1}^D \theta_i x_n^i)}}. \tag{3.28} \end{equation}La razón por la cual estoy mostrando de nuevo esta ecuación, es porque la utilizaremos, pero ahora para expresar la ecuación para obtener la probabilidad de que y_n = 0 | x_n, \theta , es decir, de que la etiqueta sea igual a 0 dado el valor de la entrada x_n y sus características, en vez de obtener la probabilidad condicional de que y_n = 1 | x_n, \theta , como se ha mostrado anteriormente.
Considerando que p(y_n = 1 | x_n, \theta) = \sigma(x_n), tenemos que
\begin{equation} p(y_n = 0 | x_n, \theta) = 1 - \sigma(x_n), \tag{3.46} \end{equation}lo cual no es más que el complemento de la probabilidad, donde 1-(probabilidad de que el dato pertenezca a la clase 1), es la probabilidad restante correspondiente a que el dato corresponda a la clase 0.

Bien, ahora pasemos a lo mágico.
La probabilidad condicional de que y_n sea igual a 1 o 0 se puede escribir de manera compacta utilizando las Ecuaciones (3.28) y (3.46). Esto se hace elevando \sigma(x_n) a la potencia y_n y (1 - \sigma(x_n)) a la potencia (1 - y_n) , quedando
\begin{equation} p(y_n | x_n, \theta) = \sigma(x_n)^{y_n} \cdot (1 - \sigma(x_n))^{1 - y_n}. \tag{3.47} \end{equation}El por qué de esta expresión y sus potencias lo desglosaremos a continuación. Esta ecuación, la (3.47), es el núcleo de la función de pérdida de entropía cruzada binaria, y comprender el por qué tiene esa forma nos dirá todo sobre su funcionamiento para evaluar un modelo clasificador binario de aprendizaje automático.
La idea central es que, debido a la naturaleza binaria de y_n (su par de etiquetas para clasificación), las expresiones \sigma(x_n)^{y_n} y (1 - \sigma(x_n))^{1 - y_n} seleccionan la probabilidad correcta conforme se tiene y_n = 1 o y_n = 0 en (3.47),
Para entenderlo, desarrollemos cada caso:
1. Cuando y_n = 1 :
\begin{equation}y_n = 1 \implies 1 - y_n = 0, \tag{3.48} \end{equation}por lo tanto, la Expresión (3.47) se convierte en:
\begin{aligned}\sigma(x_n)^1 \cdot (1 - \sigma(x_n))^0 &= \sigma(x_n) \cdot 1 \\
&= \sigma(x_n). \tag{3.49} \end{aligned}Esta expresión es correcta porque \sigma(x_n) es, por definición, la probabilidad condicional de que y_n = 1 , dado x_n y los parámetros \theta , recordémoslo:
\begin{equation} p(y_n = 1 | x_n, \theta) = \sigma(x_n). \tag{3.50} \end{equation}2. Cuando y_n = 0 :
\begin{equation}y_n = 0 \implies 1 - y_n = 1, \tag{3.51} \end{equation}lo cual que significa que la Ecuación (3.47) se convierte en:
\begin{aligned}\sigma(x_n)^0 \cdot (1 - \sigma(x_n))^1 &= 1 \cdot (1 - \sigma(x_n)) \\
&= 1 - \sigma(x_n), \tag{3.52} \end{aligned}Lo cual sabemos que es correcto, dado que es su complemento, como definimos en (3.46).
De esto se concluye, entonces, que la expresión compacta:
\begin{equation} p(y_n | x_n, \theta) = \sigma(x_n)^{y_n} \cdot (1 - \sigma(x_n))^{1 - y_n}, \tag{3.53} \end{equation}es algebraicamente correcta porque selecciona la probabilidad correcta dependiendo del valor de y_n . Es equivalente a las dos probabilidades de las clases definidas, por lo que proporciona una forma unificada para calcular la probabilidad condicional de la clase correcta, ya sea y_n = 0 o y_n = 1 .



Maximización de la verosimilitud
Sabemos que la regresión logística busca ajustar los parámetros \theta del modelo \sigma(x_n) para maximizar la probabilidad de que el modelo prediga correctamente las clases a las que pertenecen las observaciones dadas las entradas. Esto se llama maximización de la verosimilitud (Maximum Likelihood Estimation, MLE), y ya la hemos estudiado con anterioridad.
Para calcular la máxima verosimilitud, se debe considerar la probabilidad conjunta de todas las observaciones, la cual por definición sabemos que es el producto de las probabilidades individuales:
\begin{equation}
P(\mathbf{y}|\mathbf{x}, \theta) = \prod_{n=1}^N p(y_n | x_n, \theta), \tag{3.54}
\end{equation}donde N es el número total de observaciones.
Trabajar con el producto de probabilidades puede ser numéricamente inestable y complicado. Para simplificar las derivadas y la optimización, se toma (como ya es costumbre) el logaritmo de la probabilidad conjunta. El logaritmo transforma el producto en una suma, que es más manejable:
\begin{equation}
\log P(\mathbf{y}|\mathbf{x}, \theta) = \sum_{n=1}^N \log p(y_n | x_n, \theta). \tag{3.55}
\end{equation}Por último, en lugar de maximizar la probabilidad logarítmica, minimizamos su opuesto, que es equivalente. De aquí surge la función de pérdida logarítmica (log-loss). Tomar el negativo del logaritmo asegura que estamos minimizando una cantidad positiva cuando las predicciones son buenas (alta probabilidad) y castigando más fuertemente las malas predicciones (baja probabilidad):
\begin{equation}
l(y_n, \sigma(x_n)) = -\log(p(y_n | x_n, \theta)). \tag{3.56}
\end{equation}Utilizando la expresión compacta de la probabilidad condicional de la Ecuación (3.47), sustituimos en (3.56) y obtenemos:
\begin{equation}
l(y_n, \sigma(x_n)) = -[y_n \log(\sigma(x_n)) + (1 - y_n) \log(1 - \sigma(x_n))], \tag{3.57}
\end{equation}Si lo piensas bien, esta expresión ya la habíamos avistado antes; revisa la Ecuación (3.36) de la exploración de la regresión logística.
Finalmente, calculamos el promedio de estas pérdidas individuales para obtener la función de pérdida:
\begin{aligned} L(\mathcal{Y}, \mathcal{\hat{Y}})) = \frac{1}{N} \sum_{n=1}^N l(y_n, \sigma(x_n)) \end{aligned}, \tag{3.58}Con esto queda demostrado cómo es que la función de pérdida refleja las probabilidades calculadas por el modelo dados los distintos valores de las clases.
Lo ilustraremos con un ejemplo.
Ejemplo de aplicación de función de pérdida logística
Volvamos a nuestro ejemplo en el que hemos entrenado un modelo de clasificación de alumnos dadas sus horas dedicadas de estudio, y calculemos la probabilidad de que un par de observaciones pertenezcan a la clase 1 (examen aprobado).
Dado que tenemos solo una variable independiente (horas de estudio), nuestro modelo es una función sigmoidea univariable como la que se ha definido en la Ecuación (3.29):
\begin{aligned}
\sigma(x_n)=\frac{1}{1+e^{-(\theta_{0}+\theta_{1}x_n)}}\:. \tag{3.29}
\end{aligned}Aquí ya usaremos de forma explícita las ecuaciones y valores involucrados en el proceso. Supongamos que después de ajustar los parámetros del modelo en la fase de entrenamiento, hemos obtenido los siguientes valores:
\theta_0 = -2
\theta_1 = 1
Dando como resultado la función:
\begin{aligned}
\sigma(x_n)=\frac{1}{1+e^{-((-2)+1(x_n))}}\:. \tag{3.59}
\end{aligned}Las dos observaciones que utilizaremos de nuestro conjunto de datos son las siguientes:
| Horas de estudio (x_n) | Valor real de su etiqueta/clase (y_n) |
| 1 | 0 |
| 4 | 1 |
Para hacer uso de la función de pérdida logística primero calcularemos las predicciones del modelo para las dos entradas univariables.
Comenzamos con el primer dato x_1 = 1 :
\begin{aligned} \sigma(x_1) = \frac{1}{1 + e^{-((-2) + 1(1))}} = \frac{1}{1 + e^{1}} \approx 0.268. \tag{3.60} \end{aligned}Para x_2 = 4 :
\begin{aligned} \sigma(x_2) = \frac{1}{1 + e^{-((-2) + 1(4))}} = \frac{1}{1 + e^{-2}} \approx 0.88. \tag{3.61}\end{aligned}Ahora que hemos calculado las probabilidades, utilizamos la función de entropía cruzada para obtener la pérdida de las predicciones del modelo, comparando las predicciones dada cada entrada con su respectiva etiqueta real (clase a la que pertenece).
Para la entrada x_1 = 1 con la etiqueta real y_1 = 0 , sustituimos en la Ecuación (3.57), la cual es la función de pérdidas individuales de la regresión logística:
\begin{align*}
L(y_2, \sigma(x_2)) &= - \left[0 \cdot \log(0.268) + (1 - 0) \cdot \log(1 - 0.268)\right] \\
&= - \log(0.732) \\
&\approx 0.311. \tag{3.62}
\end{align*}Lo hacemos ahora para x_2 = 4 con y_2 = 1 :
\begin{align*}
L(y_1, \sigma(x_1)) &= - \left[1 \cdot \log(0.88) + (1 - 1) \cdot \log(1 - 0.88)\right] \\
&= - \log(0.88) \\
&\approx 0.127. \tag{3.63}
\end{align*}Y obtenemos la pérdida total calculando el promedio:
\begin{aligned} J(\theta) = \frac{1}{2} [0.127 + 0.311] = \frac{1}{2} (0.438) \approx0.219. \tag{3.64}\end{aligned}Este valor es interpretable de acuerdo a las reglas expuestas en el tramo anterior. Dado que es de 0.219 , y que conforme la pérdida calculada tienda a 0 la precisión del modelo es mayor, se puede concluir que el modelo tiene un rendimiento aceptable.
Conociendo el cómo operan las funciones de pérdida para modelos de clasificación y regresión, podemos comenzar a explorar cómo funcionan algoritmos de aprendizaje supervisado más complejos, y utilizarlas también para evaluar el rendimiento final de los modelos ajustados al terminar la fase de entrenamiento, lo cual veremos de forma más detallada en la siguiente travesía.



Hola! solo me gustaría externar mi enorme agradecimiento por esta clara y concisa explicación. Espero que sigas haciendo desarrollando y publicando temas de interés! Saludos
Muchas gracias! Por estos comentarios sigo adelante 😀