Uno de los conceptos medulares del machine learning es el de funciones de pérdida, las cuales son un componente esencial de cualquier algoritmo de aprendizaje supervisado, e incluso hacen acto de presencia en otros tipos de algoritmos, como los de aprendizaje no supervisado. Como una preparación previa al estudio de las redes neuronales artificiales, comenzaremos a revelar este y otros conceptos relacionados al aprendizaje de máquinas; en este caso, se trata de un ingrediente esencial para el proceso de entrenamiento y evaluación de modelos.

Inventario recomendado

Matemáticas
Un poco de álgebra y cálculo

Regresión lineal (definición de algoritmos de regresión)

Regresión logística (definición de algoritmos de clasificación)

Algún bocadillo

Funciones de pérdida para aprendizaje de máquinas

Como ya hemos visto en la teoría y práctica de la regresión lineal y la regresión logística, al momento de entrenar un modelo de aprendizaje supervisado se está ejecutando un proceso que ajusta los valores de sus parámetros utilizando una función que mide qué tan grande es la distancia entre las estimaciones realizadas por el modelo y los datos reales (también conocidos como datos del terreno real, o verdad fundamental); dichas funciones se conocen como funciones de pérdida.
Dicho de una forma más concisa, una función de pérdida, función de error, o función de costo (loss function), es una función matemática que evalúa el desempeño de un modelo de aprendizaje automático calculando las diferencias entre los valores predichos por este, y los valores reales del conjunto de datos.
Esta función es vital para el entrenamiento del modelo, ya que de esto depende el ajuste/optimización de sus parámetros, y generalmente, ofrece una forma para la evaluación de los resultados finales.


Es correcto, dado que el modelo es puesto a prueba por la función de pérdida, esta evalúa la calidad de los parámetros de la función ajustada durante y después de la etapa de entrenamiento.
La Figura 3.4.1 muestra en términos sencillos cómo opera una función de costo, calculando las diferencias entre los valores obtenidos por el modelo, y las observaciones del conjunto de datos:
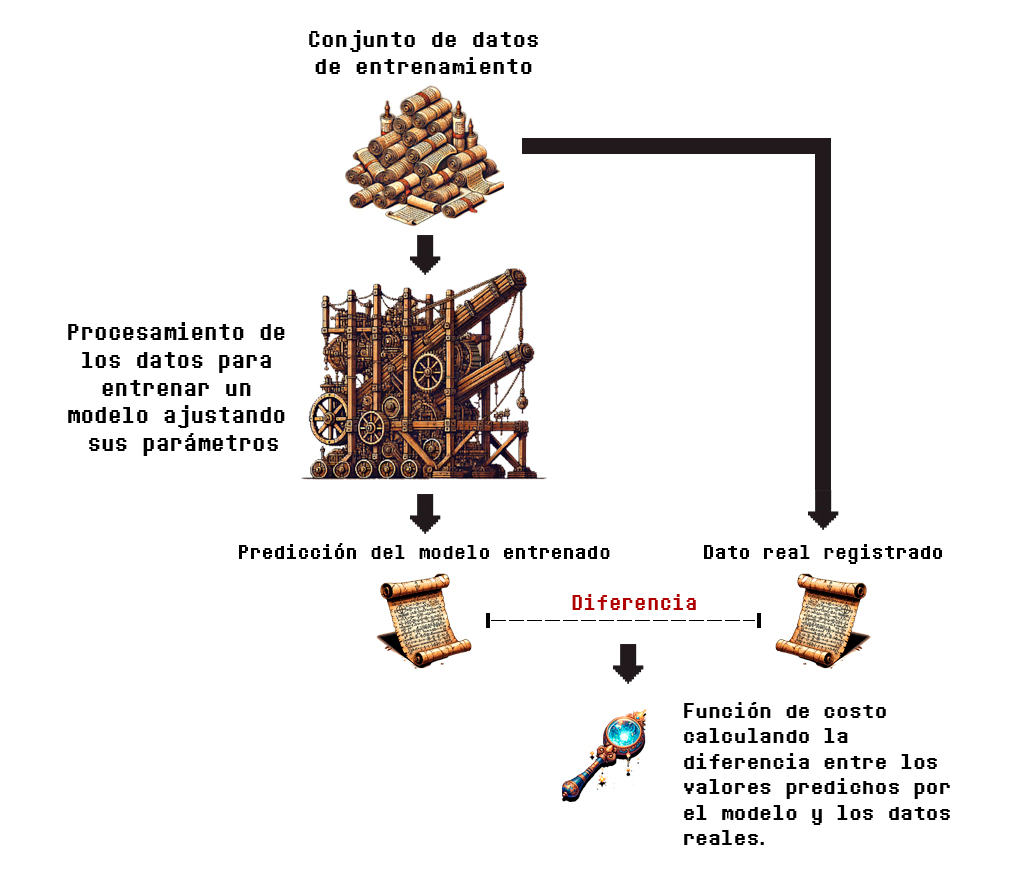
Es importante mencionar que las funciones de pérdida se pueden utilizar tanto durante la etapa de aprendizaje (ajuste de parámetros) como después, cuando el modelo ya ha sido entrenado.
Las funciones de costo que hemos visto hasta ahora son utilizadas para optimizar los parámetros en la fase de entrenamiento, pero conforme avancemos en el curso las utilizaremos también para evaluar el modelo final resultante.
A continuación, exploraremos el objetivo y uso de las funciones de pérdida con mayor detalle.
Ejemplo de una función de pérdida
Uno de los ejemplos más comunes de una función de pérdida, y que ya hemos visto en acción en la práctica de la regresión lineal, es la función de error cuadrático medio (MSE, por sus siglas en inglés: Mean Squared Error), la cual calcula el promedio del cuadrado de las diferencias entre los valores del terreno real y los valores predichos.

Vamos a ilustrarlo poco a poco.
Supongamos que hemos ajustado los parámetros de un modelo utilizando técnicas de aprendizaje de máquinas, específicamente, un modelo de aprendizaje supervisado que aborda un problema de regresión. La siguiente tabla contiene los valores reales del conjunto de datos y las cantidades estimadas por el modelo resultante.
| Valores reales | Valores predichos |
|---|---|
| 12 | 11 |
| 15 | 13.5 |
| 19 | 21 |
| 21.5 | 24 |
| 33 | 32 |
| 37 | 35.5 |
| 40 | 38 |
| 42.5 | 42.5 |
| 45 | 43.8 |
| 49 | 50 |
Ahora calcularemos el error cuadrático medio (la función de costo), paso por paso:
- De acuerdo con la definición, primero se calcula la diferencia entre los valores reales y los valores predichos, lo cual quedaría como se muestra en la nueva columna añadida:
| Valores reales | Valores predichos | Diferencia |
|---|---|---|
| 12 | 11 | 1 |
| 15 | 13.5 | 1.5 |
| 19 | 21 | -2 |
| 21.5 | 24 | -2.5 |
| 33 | 32 | 1 |
| 37 | 35.5 | 1.5 |
| 40 | 38 | 2 |
| 42.5 | 42.5 | 0 |
| 45 | 43.8 | 1.2 |
| 49 | 50 | -1 |
- Ahora que tenemos las diferencias, obtendremos el cuadrado de estas:
| Valores reales | Valores predichos | Diferencia | Cuadrado de las diferencias |
|---|---|---|---|
| 12 | 11 | 1 | 1 |
| 15 | 13.5 | 1.5 | 2.25 |
| 19 | 21 | -2 | 4 |
| 21.5 | 24 | -2.5 | 6.25 |
| 33 | 32 | 1 | 1 |
| 37 | 35.5 | 1.5 | 2.25 |
| 40 | 38 | 2 | 4 |
| 42.5 | 42.5 | 0 | 0 |
| 45 | 43.8 | 1.2 | 1.44 |
| 49 | 50 | -1 | 1 |
- Teniendo estas diferencias, solo debemos añadir dos pasos más, primero sumamos los valores de esta última columna:
- Suma del cuadrado de las diferencias = 23.19
- Y por último, calculamos el promedio, es decir, dividimos esta suma entre el número de valores o datos, el cual es 10:
- Suma del cuadrado de las diferencias dividida entre el total de datos = \frac{23.19}{10} = 2.319.
Esto quiere decir que el error cuadrático medio (valor arrojado por la función de costo) del modelo es aproximadamente 2.31.
De esta forma, el algoritmo calcula qué tanto se acercan las predicciones del modelo a las cifras reales. Dado que el rango de los valores reales está entre 11 y 50, podemos intuir que un promedio de 2.31 de los errores es relativamente pequeño, por lo que se puede aseverar que tiene un desempeño aceptable (estas conclusiones siempre dependerán de los datos, es necesario recordar, en general, que conforme esta métrica se acerca a 0, indica una mejor precisión del modelo).
Dentro de los algoritmos de regresión lineal y logística, recordemos que lo que se hace es optimizar estas funciones, es decir, minimizar o maximizar sus resultados (dependiendo de la función utilizada); por ejemplo, en la regresión lineal se busca minimizar el MSE, de modo que se ajustan los parámetros para encontrar el valor más pequeño posible de los errores medidos por esta función (los mismos que acabamos de calcular). En este sentido, minimizar es optimizar, ya que con ello se encuentran los parámetros más óptimos para generar un modelo eficiente.
El ejemplo atestiguado hasta ahora se centra en una función de pérdida aplicado a un modelo de regresión; con el fin de no extender mucho esta lección, no analizaremos el procesamiento generado por una función de pérdida para modelos de clasificación (para los cuales, de cualquier manera, el principio operacional es el mismo). Esto lo examinaremos con más detalle en la siguiente exploración.
Habiendo ilustrado cómo opera una función de costo y cuál es su uso, echemos un vistazo a los tipos de funciones de pérdida que existen, y una lista con ejemplos de cada uno.
Tipos de funciones de pérdida
Las funciones de error son variadas y se utilizan dependiendo de los conjuntos de datos de entrada y el contexto del propósito del modelo de aprendizaje automático. Se dividen principalmente en dos categorías:
- Funciones de pérdida para aprendizaje supervisado, que a su vez se subdividen de acuerdo al tipo de modelo:
- Modelos de regresión.
- Modelos de clasificación.
- Funciones de pérdida para aprendizaje no supervisado.

Es verdad, sin embargo, es importante al menos saber que estas funciones existen no solo para un tipo de machine learning. Por lo mismo, a continuación dejaré unas listas con las funciones de error más comunes; en las prácticas de programación no utilizaremos todas, pero puede que en algún momento necesites información sobre algunas de las funciones disponibles, ya sea en el ámbito laboral, personal o académico.
Funciones de pérdida más utilizadas para machine learning
A continuación, enlistaré las funciones de pérdida más comunes para machine learning por categorías, no te preocupes si te parecen cuantiosas, en la práctica solo utilizarás algunas cuantas, solo quiero que conozcas su existencia y sea una referencia que puedas tener a la mano.
Funciones de pérdida para aprendizaje supervisado
Funciones de pérdida para algoritmos de regresión
Las funciones de pérdida más comunes para modelos de regresión son las siguientes:
- Error cuadrático medio (Mean Squared Error, MSE).
- Error absoluto medio (Mean Absolute Error, MAE).
- Error absoluto porcentual medio (Mean Absolute Percentage Error, MAPE)
- Raíz del error cuadrático medio (Root Mean Square Error, RMSE).
- Raíz del error logarítmico cuadrático medio (Root Mean Squared Logarithmic Error, RMSLE).
- Pérdida de Huber (Huber Loss).
- Pérdida Log-cosh. (Log-Cosh Loss).
- Pérdida cuantílica (Quantile Loss).
- L1 suavizado (Smooth L1).
- Pérdida ∈-insensible (∈-Insensitive Loss).
Funciones de pérdida para algoritmos de clasificación
Las funciones de pérdida más comunes para modelos de clasificación son las siguientes:
- Pérdida de entropía cruzada (Cross Entropy Loss).
- Pérdida de entropía cruzada sigmoidea (Sigmoid Cross Entropy Loss).
- Pérdida de entropía cruzada softmax (Softmax Cross Entropy Loss).
- Verosimilitud logarítmica negativa (Negative Log-Likelihood).
- Pérdida 0-1 (0-1 Loss).
- Pérdida de Hinge (Hinge Loss).
- Pérdida Huber modificada (Modified Huber Loss).
- Pérdida de Hinge suavizada (Smooth Hinge Loss).
- Pérdida de Hinge reescalada (Rescaled Hinge Loss).
- Pérdida de rampa (Ramp Loss).
- Erro de clasificación mínimo (Minimum Classification Error).
- Pérdida logarítmica (Log Loss).
- Pérdida exponencial (Exponential Loss).
- Pérdida basada en margen (Margin-Based Loss).
- Ranqueo por parejas (Pairwise Ranking).
- Ranqueo por tripleta (Triplet Ranking).
- Pérdida contrastiva (Contrastive Loss).
- Pérdida pinball (Pinball Loss).
- Pérdida pinball truncada (Truncated Pinball Loss).
Funciones de pérdida para aprendizaje no supervisado
Las funciones de pérdida más comunes para evaluar el desempeño de algoritmos de aprendizaje no supervisado son las siguientes:
- Error cuadrado (Square Error).
- Error de distancia (Distance Error).
- Error de reconstrucción (Reconstruction Error).
- Varianza negativa (Negative Variance).
- Pérdida de energía (Energy Loss).
- Pérdida minimax (Minimax Loss).
- Pérdida de Wasserstein (Wasserstein Loss).
- Función de pérdida de difusión (Diffusion Model Loss Function).
Para más información sobre estas funciones y sus respectivas definiciones matemáticas, puedes consultar los siguientes recursos:
- A survey and taxonomy of loss functions in machine learning.
- A Comprehensive Survey of Loss Functions in Machine Learning.
Teniendo esto en mente, ya has conocido lo suficiente para tener una idea del uso y definición de una función de pérdida. Ahora lo formalizaremos matemáticamente.
Función de perdida, definición matemática

Como habrás notado, las funciones de pérdida son parte medular de nuestros encuentros con gran parte de los algoritmos de aprendizaje automático; su objetivo es generar una medida de qué tan bien opera un modelo entrenado, o en proceso de entrenamiento, para realizar estimaciones numéricas.
Por ello, se puede definir una generalización matemática de esta función, que expresa la idea central de su finalidad y los cálculos que conducen al cumplimiento de su objetivo.
Definición 3.10 (Función de Pérdida). Sea \mathcal{D} = \lbrace (x_{1},y_{1}),…,(x_{N},y_{N})\rbrace un conjunto de N datos u observaciones etiquetadas compuesto por los conjuntos \mathcal{X} = \lbrace x_{1},…, x_{N}\rbrace de entradas y \mathcal{Y} = \lbrace y_{1},…, y_{N}\rbrace de salidas, utilizado para entrenar un modelo o función h(x), donde cada salida del modelo se expresa como h(x)=\hat{y}. Una función de pérdida es un mapeo que toma un valor verdadero y \in \mathcal{Y} y un valor predicho \hat{y}, y asigna a esta pareja un número real que cuantifica el «error» o «pérdida» del modelo h(x) que ha hecho la predicción \hat{y} .
En términos generales, la función de pérdida para la evaluación de un modelo dado un conjunto de datos \mathcal{D} con N instancias se define como sigue:
L(\mathcal{Y}, \mathcal{\hat{Y}}) = \frac{1}{N} \sum_{n=1}^N l(y_n, \hat{y}_n) , \tag{3.42}donde \mathcal{\hat{Y}} es el conjunto de todas las predicciones realizadas con el modelo y que están sometidas a evaluación, y l es una función de pérdidas individuales, es decir, la medición del error o distancia entre la predicción \hat{y}_n y su valor y_n real asociado. La forma de agregación, en este caso, expresada mediante la suma \sum, puede variar, así como N puede ser igual a 1 para mantener solo la agregación sin calcular el promedio.
Nota: sin entrar en más detalle, solo se hará mención de que en algunos casos especiales (como en los autoencoders, los cuales definiremos en otra exploración) se tiene que X = Y, pero que esto no desvíe tu atención de la definición antes presentada.
Taxonomía y ejemplo de una función de pérdida
Para digerir más fácilmente esta definición, retomaremos el ejemplo del error cuadrático medio (ECM), ahora relacionando su estructura respecto a la generalización de la función de pérdida de la Definición 3.10. Para esto, identificamos los elementos de su taxonomía como sigue:
- Agregador de pérdidas o errores: el cual viene señalado en la Ecuación (3.42) como \frac{1}{N} \sum_{n=1}^N.
- Función de pérdidas individuales: la cual viene expresada en la Ecuación (3.42) como l(y_n, \hat{y}_n).
Ahora, echemos un vistazo a la definición matemática del error cuadrático medio:
L(\mathcal{Y}, \mathcal{\hat{Y}}) = \frac{1}{N} \sum_{n=1}^N (y_n - \hat{y}_n)^2 \tag{3.43}¿Puedes identificar los elementos antes descritos en esta última expresión?
Si revisamos cuidadosamente encontramos lo siguiente:
- Agregador de pérdidas: \frac{1}{N} \sum_{n=1}^N
- Función de pérdidas individuales: (y_n - \hat{y}_n)^2
Podemos observar cómo se promedian los resultados de la función de pérdidas individuales, lo cual es el mismo cálculo que desglosamos en el ejemplo de la sección anterior.
Para ilustrarlo mejor, podemos, por ejemplo, obtener el valor de la pérdida para los primeros cinco valores de la Tabla 3.4.1 utilizando la expresión (3.43):
L(y, \hat{y}) = \frac{1}{N} \sum_{n=1}^N (y_n - \hat{y}_n)^2=\frac{(12-11)^2+(15-13.5)^2+(19-21)^2+(21.5-24)^2+(33-32)^2}{5}=\frac{1+2.25+4+6.25+1}{5}=\frac{14.5}{5} =2.9Esto significa que el valor de la función de pérdida para los primeros 5 valores respecto a las predicciones del modelo es igual a 2.9. Nótese cómo este número es el resultado de mapear las salidas del conjunto de entrenamiento y las predicciones a un número real, que refleja la similitud entre estas.
Aquí damos por finalizado el estudio de este invaluable artefacto de la ciencia de datos. Aún no veremos cómo obtener los valores de las funciones de pérdida con Python, esto lo haremos más adelante cuando las utilicemos para evaluar el rendimiento de modelos de aprendizaje supervisado.

En la siguiente expedición aprenderemos cómo opera una función de pérdida para la evaluación de modelos de clasificación, lo cual nos abrirá paso a formas más robustas de evaluación de rendimiento de modelos.



Has puesto dos veces seguidas «los». Y esto parece incorrecto: «Es verdad, sin embargo, es importante al menos sabe». Gracias por el artículo! Saludos desde Guadalajara en España.
Gracias, Javier! Eso me ayuda mucho, tengo problemas de atención al escribir. Saludos desde Guadalajara, México 🙂
En el primero parrafo hay un error: “se trata de trata de”
Increíble, yo pensé que ya no había detalles jajajaja gracias por ayudarme! Cualquier cosa que vean, sin piedad coméntenla
Está mal la definición de función de pérdida en los índices.
Qué tal, Erick! Creo que te refieres a las «i» y «n» que tenía mezcladas en los subíndices en la definición matemática, es verdad, he realizado la corrección, gracias