Entre la diversa gama de algoritmos del machine learning, la regresión lineal es, probablemente, al menos en lo que respecta al aprendizaje supervisado, el más elemental. Esta técnica es bastante útil para realizar inferencias sobre datos cuyas variables que los describen guardan aparentes relaciones lineales entre sí; su uso abarca tanto los ámbitos científicos y empresariales, y es un componente básico de algoritmos más complejos y con mayor relevancia en la actualidad como las redes neuronales artificiales (que a su vez son la partícula elemental de los avances más grandes en IA actualmente), por lo que su estudio fungirá como un puente hacia la inspección de varias definiciones relevantes del aprendizaje de máquinas.
En esta exploración te mostraré todo lo que necesitas saber sobre la regresión lineal: su significado, funcionamiento, definición matemática, y otras peculiaridades a tomar en cuenta para su correcta aplicación para el análisis de datos inferencial. Todo esto lo pondrás en práctica con un programa en Python, el cual tiene un enfoque hacia la resolución de un problema en el que utilizaremos datos reales.
Este será tu primer acercamiento a un algoritmo de machine learning cimentado desde su definición hasta la resolución de problemas utilizándolo para modelar patrones de un conjunto de datos.

Equipaje recomendado


Fundamentos del aprendizaje supervisado


Programación en Python

Matemáticas
Álgebra, probabilidad, estadística, y las definiciones dadas en nuestro acercamiento al aprendizaje supervisado.

Algun acompañamiento

*Notas:
1. Debido a las necesidades que debemos cubrir antes de iniciar nuestro encuentro con la regresión lineal en Python, la sección de matemáticas esta vez aparecerá precediendo a la de programación.
2. Esta travesía develará principalmente el funcionamiento de la regresión lineal simple/univariable. La teoría que corresponde a su versión multivariable se considerará de manera breve en la sección de matemáticas.
Regresión lineal, la madre de los algoritmos del machine learning

Como ya se ha mencionado, la regresión lineal es uno de los corpúsculos que componen la base del aprendizaje automático; el tipo de fenómenos que es capaz de modelar puede ser de cualquier índole, y ha sido extensamente utilizada desde hace más de dos siglos.
Su esencialidad para el desarrollo ulterior de la teoría del aprendizaje de máquinas no la dota de una simplicidad exenta de la teoría matemática, ya que nace y se desarrolla puramente a través de ella. Sin embargo, es posible explicar sus usos y los principios de su método sin aludir explícitamente a este campo.
Como ha sucedido en nuestros recorridos hasta ahora, primero exploraremos su definición de una manera no rica en tecnicismos, con ejemplos e ilustraciones complementarias, y después desglosaremos su forma matemática.
Para empezar a tantear los terrenos pertenecientes a la regresión lineal, en esta ocasión partiremos desde un ejemplo, y lo iremos desarrollando hasta introducir la idea general de su funcionamiento y objetivo, para lo cual supondremos un nuevo misterio a ser abordado.
Regresión lineal: planteamiento del problema
El cuestionamiento a atacar en esta ocasión es el siguiente: dada una tabla con información sobre las horas de estudio de un grupo de alumnos y su calificación obtenida, ¿cómo podemos estimar la calificación de un alumno dado el número de horas que destinó a estudiar?
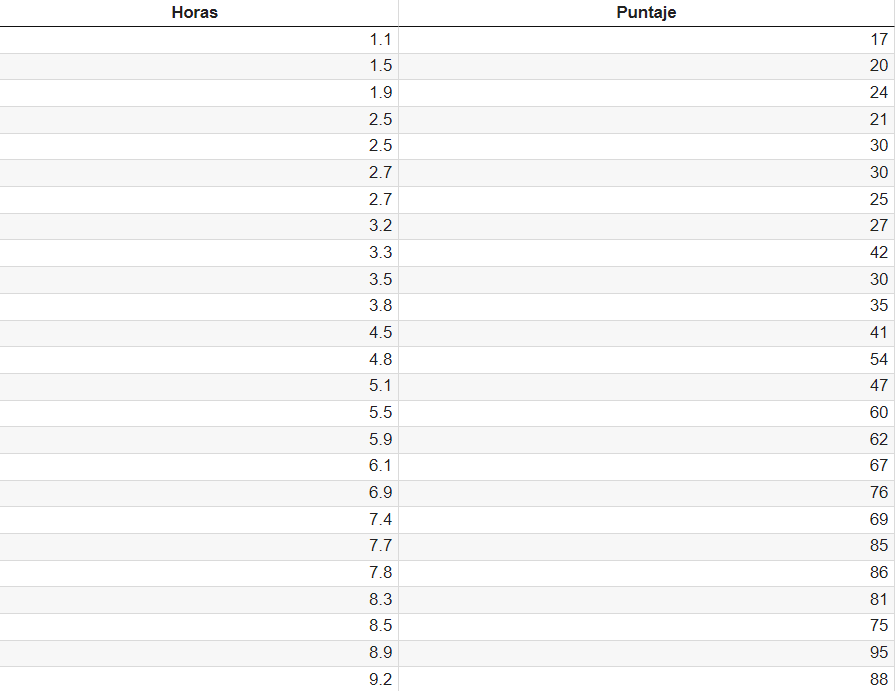
En la Tabla 3.2.1 se puede observar el conjunto de datos en su forma tabular, la cual nos permite discernir la relación que guarda el puntaje obtenido por los alumnos con las horas que han dedicado al estudio.
Para poder vislumbrar más claramente el tipo de relación existente entre nuestras entradas y salidas, emplearemos uno de los principales métodos para explorar un conjunto de datos cuando este consta de dos o tres variables, y del cual hemos hablado en la excursión sobre análisis exploratorio de datos: observar su dispersión en una gráfica.
En este caso, utilizaremos un sencillo plano en el que dibujaremos los puntos correspondientes a los valores del puntaje obtenido respecto a las horas dedicadas.
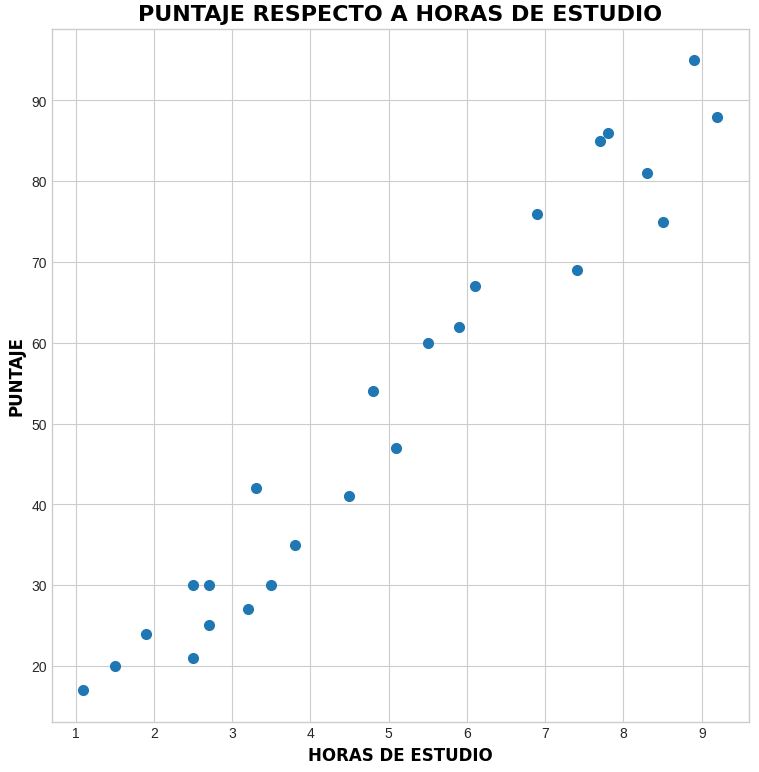
¿Qué es lo que podemos percibir en la Figura 3.2.1 respecto a la relación entre ambas variables? A simple vista, podemos identificar un patrón entre la forma en que se dan los puntajes obtenidos respecto a las horas de estudio: pareciera que se asocian dibujando una especie de línea recta con tendencia creciente (a mayores horas de estudio, mejor calificación).

Sí, se trata de la misma técnica exhibida en el ejemplo utilizado para ilustrar el aprendizaje supervisado, pero esta vez desglosaremos cómo funciona el método en su totalidad.
Sabemos que el machine learning, y más específicamente, el aprendizaje supervisado, busca la obtención <<automática>> de patrones en conjuntos de datos etiquetados, los cuales pueden ser descritos mediante funciones matemáticas. Para casos como este, en el que se atisba una relación lineal entre un par de variables, nuestro objetivo es hallar la expresión matemática que dibuje la línea recta que describa de manera más aproximada el comportamiento de nuestros datos, y esto es justo lo que podemos hacer utilizando la regresión lineal.

Ya que hemos identificado por qué esta técnica nos puede servir para nuestros fines, pasaremos a su definición.
¿Qué es la regresión lineal?
En términos sencillos, la regresión lineal es un método matemático para encontrar los parámetros de la ecuación de una recta que describe de manera aproximada la relación entre una variable dependiente y una variable independiente.


La definición más concreta es la que se expresa matemáticamente, pero esta forma la veremos en su sección correspondiente; por el momento, contemplaremos cómo luce el resultado de esta técnica, y qué usos le podemos dar.
Ejecución y resultados de la regresión lineal simple
Volvamos a nuestro problema sobre la estimación de calificaciones de acuerdo a las horas de estudio. Después de haber realizado una somera exploración de nuestros datos observando su dispersión en una gráfica de dos dimensiones (Figura 3.2.1), hemos decidido que podemos utilizar la regresión lineal para la obtención de una ecuación (línea recta) que describa de manera aproximada el comportamiento de nuestros datos, y por lo tanto, nos permita realizar predicciones sobre estos.
Sin entrar aún en detalle, para la obtención de esta recta se utiliza un método matemático, de entre los cuales el más común es el denominado de mínimos cuadrados, el cual, de forma simplificada, se puede describir como una técnica que genera una recta de manera que las distancias entre los datos y esta sea la mínima posible.
No entraremos en más especificaciones por el momento, en la Figura 3.2.2 se puede observar el resultado de la aplicación del método de regresión lineal para la adquisición de una recta (y por lo tanto, su ecuación). La operación señalada como procesamiento de datos corresponde al uso de la técnica de mínimos cuadrados para el ajuste de la recta a los datos (nótese que se pueden utilizar otros métodos para su procesamiento, pero como se ha mencionado, este es el más frecuente y el que desarrollaremos más adelante).
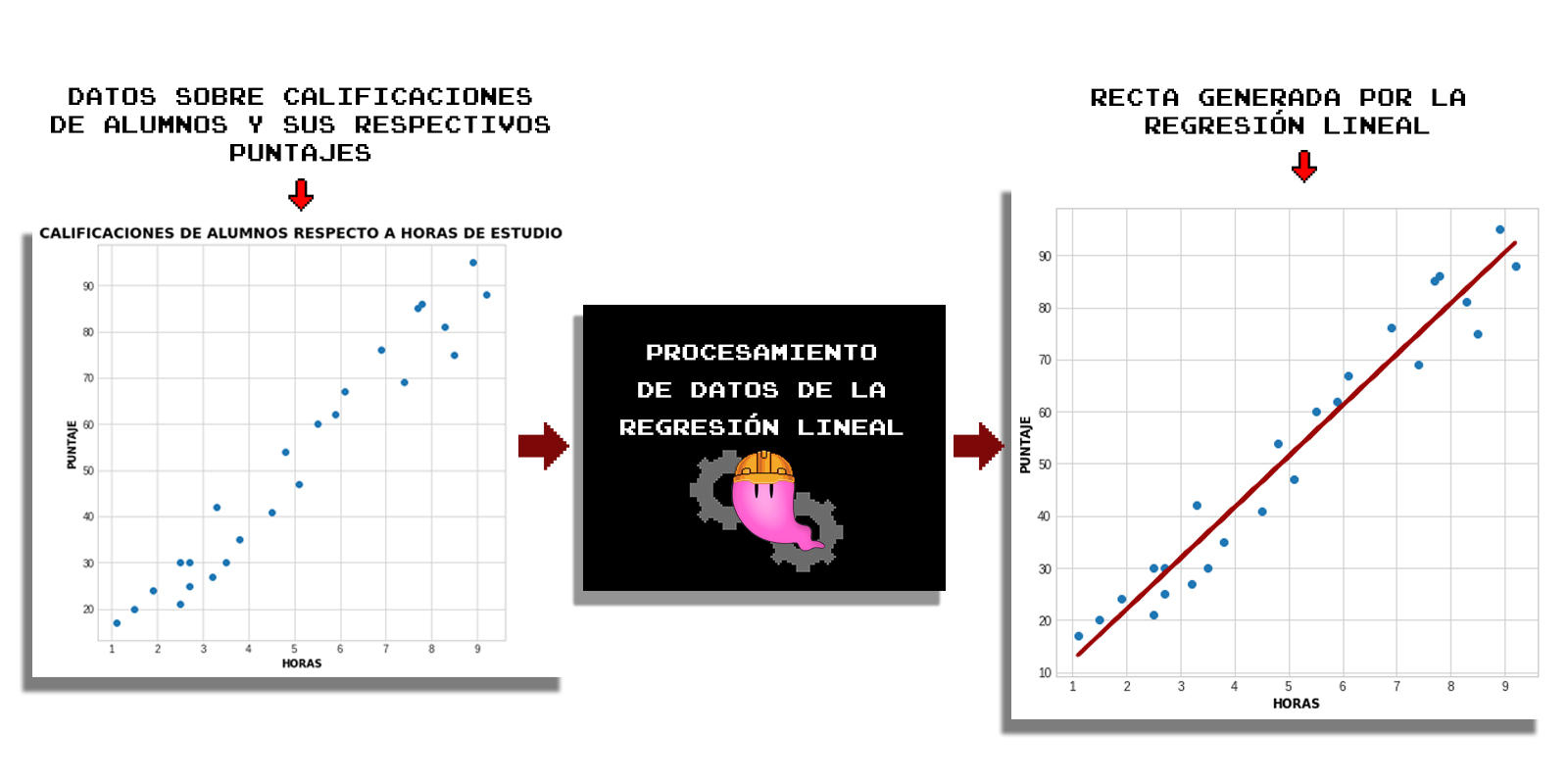
1. Entrada de datos, que en este caso se trata de un conjunto de datos de entrenamiento formado por registros de calificaciones respecto a horas dedicadas de estudio, y se ve representado en un plano por puntos dados por las relaciones entre ambas variables.
2. Procesamiento de datos, el cual corresponde a las operaciones aplicadas sobre los valores introducidos para generar un modelo predictivo (la ecuación de la recta).
3. Salida, la cual es la recta ajustada a nuestros datos, y que es dibujada por la graficación de los valores producidos por la ecuación (modelo) resultante.
Nota: como ya se ha mencionado, el resultado de la regresión lineal es una ecuación, la cual funge como modelo matemático para la estimación de valores respecto a la variable independiente. La forma y obtención de esta entidad matemática se desarrollará propiamente en la sección consiguiente.

La regresión lineal es el resultado de la aplicación del método de mínimos cuadrados para encontrar el valor de los parámetros de una ecuación lineal. Este método fue publicado por primera vez, en 1805, por el matemático francés Adrien-Marie Legendre en su libro <<Nuevos métodos para la determinación de las órbitas de los cometas>>, en el cual desarrolló un método matemático destinado a estimar los movimientos orbitales de los cometas, dados los datos de sus ubicaciones observadas.
En 1809, el titán alemán Carl Gauss publicó el mismo método para el cálculo de órbitas de cuerpos celestes, adjudicándose su creación al anunciar que lo había desarrollado alrededor del año 1795 (a la edad de 18 años).

Esto es un ejemplo (de entre muchos) de cómo científicos realizan trabajos similares en sus áreas de forma asíncrona, a veces generando altercados de todo tipo en su comunidad.


¿Cómo utilizar la regresión lineal para el análisis de datos?
Una vez que hemos obtenido una recta acoplada a nuestros datos como la mostrada en la Figura 3.2.2, podemos darle uso para obtener algún tipo de conocimiento de valor, o insight. Aquí hablaremos sobre los dos usos más comunes de la regresión lineal para el análisis de datos (descriptivo e inferencial):
- Predicción de nuevos valores.
- Identificación de tendencias.
Prediciendo datos con la regresión lineal: resolución del problema
Para abordar el primer punto, retomaremos la pregunta planteada al inicio:
- ¿Cómo podemos estimar la calificación de un alumno dado el número de horas que destinó a estudiar?
Nosotros hemos propuesto el uso de la regresión lineal para la resolución de esta cuestión, pretendiendo obtener una recta que guarde las distancias más cortas con los valores de los ejemplos de entrenamiento del conjunto de datos, y por lo tanto, utilizarla para la estimación de cantidades que no se hallan dentro de este. Esta recta se ve como sigue:
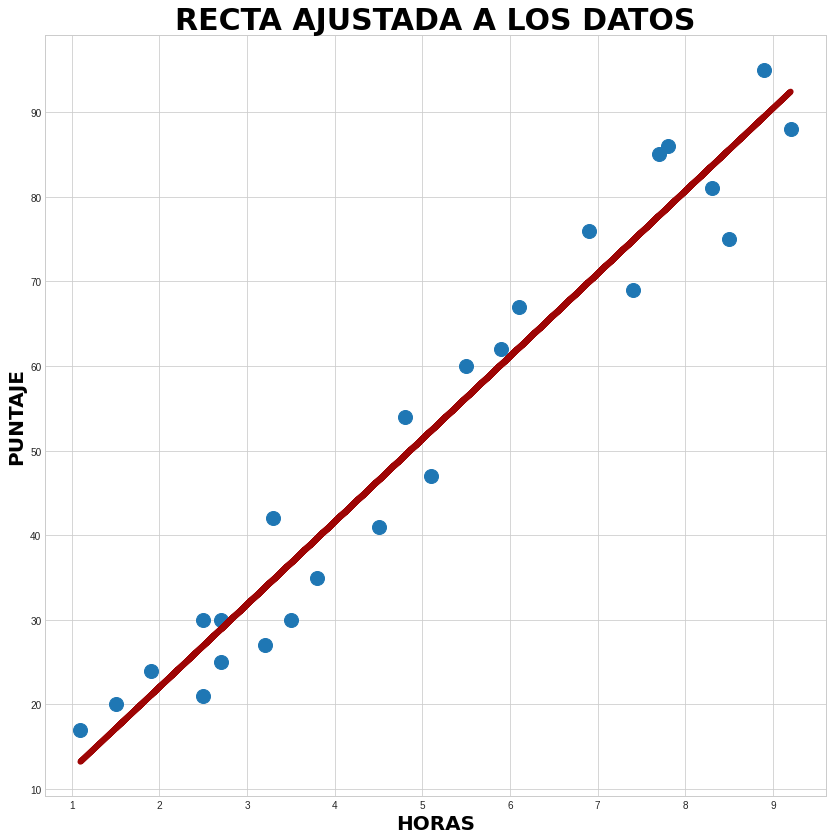
Para hacer uso de la regresión lineal aplicada, vayamos más lejos en el planteamiento de nuestra cuestión inicial haciendo una pregunta más puntual:
- ¿Cuál es el puntaje estimado para un alumno que estudió 6 horas?
Como podrás constatar en la Tabla 3.2.1, no tenemos un registro concreto de calificación para este número de horas de estudio, por lo que para hacer una aproximación del punto respecto a este valor utilizaremos el resultado obtenido por la regresión lineal. ¿Cómo lo haremos?, esto se hace identificando el valor que tiene la calificación sobre la recta en el punto que corresponde a las 6 horas de estudio.
En la Figura 3.2.4 se muestra el punto que corresponde al valor del puntaje dado por la recta en el valor de horas igual a 6:
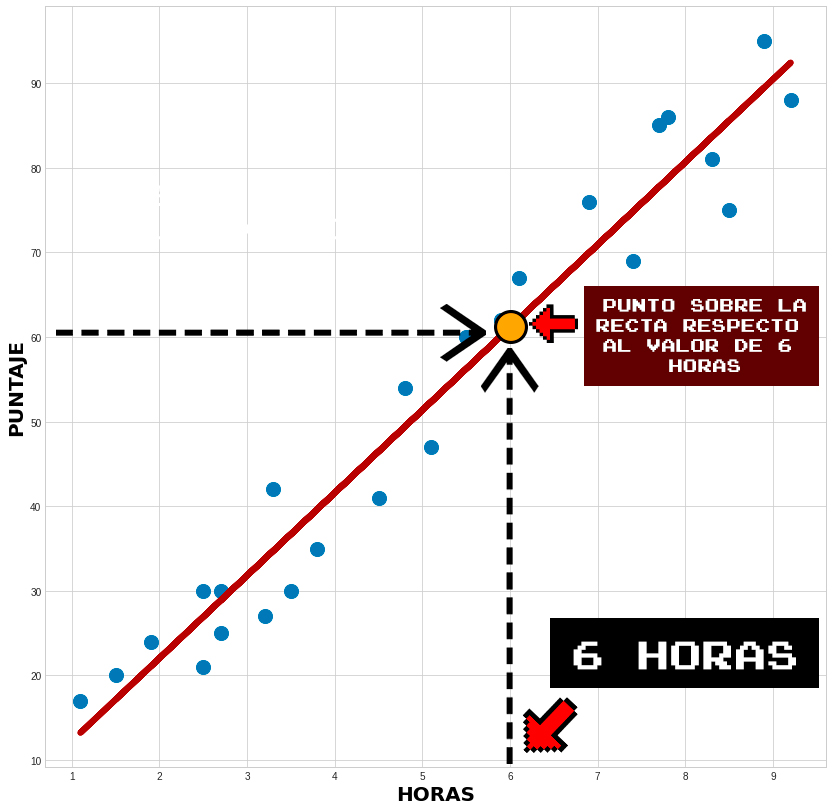
Se puede verificar cómo al identificar el número 6 en el eje horizontal, que corresponde a las horas, llegamos al punto que está sobre la recta (punto amarillo); este se sitúa aproximadamente a la altura del número 61.1 en el eje vertical, es decir, el de los puntajes. Esto se muestra de manera más concisa en la siguiente gráfica:
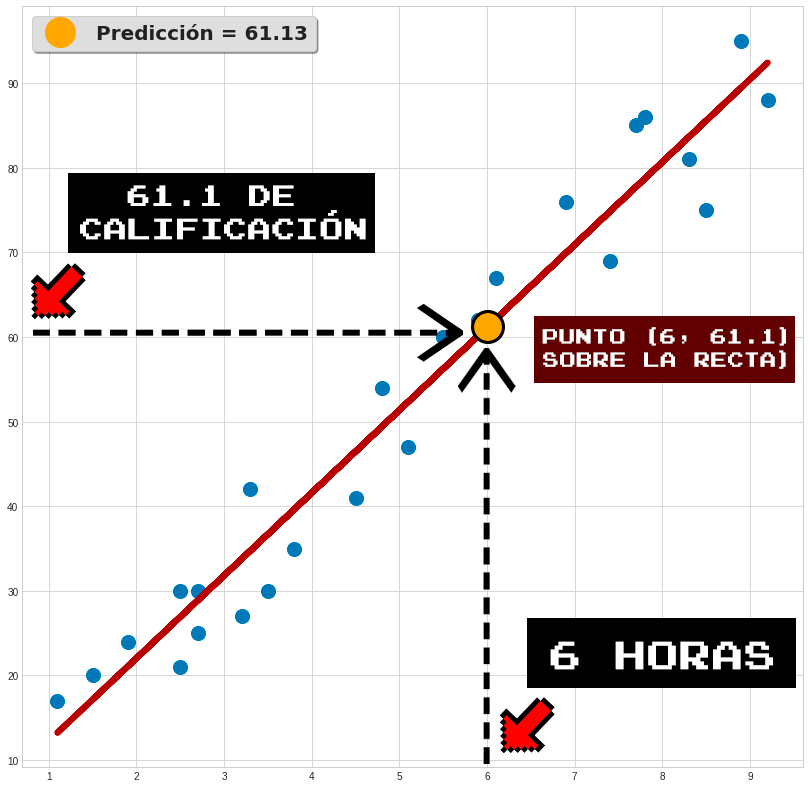
Esto quiere decir que, según la recta producida con la regresión lineal (la cual modeló un patrón intrínseco en nuestro conjunto de datos), al estudiarse 6 horas se obtendrá aproximadamente una calificación de 61.1, lo cual no difiere del comportamiento mostrado por las cantidades que ya tenemos mapeadas en la Tabla 3.2.1. Claro, esto es meramente ilustrativo, el procedimiento consiste en realidad en utilizar la ecuación de la recta obtenida para hacer las estimaciones, lo cual veremos más adelante.


Es correcto, de esta forma podemos estimar datos cuando determinamos que hay una aparente relación lineal entre estas.
Con esto que hemos trazado, ya es tiempo de responder de manera concisa a la pregunta planteada en un inicio:
¿Cómo podemos estimar la calificación de un alumno dado el número de horas que destinó a estudiar?
Nuestra respuesta a esto es que una forma de hacerlo es, dado su comportamiento aparentemente lineal, modelando una recta que se ajuste a estos datos, y utilizando el modelo resultante para predecir valores nuevos respecto a entradas nuevas, es decir, utilizando el modelo para estimar calificaciones respecto a cierto número de horas dadas.
Regresión lineal para avistar tendencias
Otra forma de utilizar la regresión lineal es para obtener un indicio de la tendencia de un conjunto de datos, es decir, si muestra un comportamiento creciente o decreciente. Varias aplicaciones que permiten visualización de datos generan y despliegan rectas obtenidas mediante regresiones lineales con la intención de denotar estas tendencias, y prácticamente solo nos muestran hacia dónde están inclinadas las rectas resultantes, es decir, su pendiente.
En las Figura 3.2.6 puedes observar dos conjuntos de datos con tendencias crecientes y decrecientes:
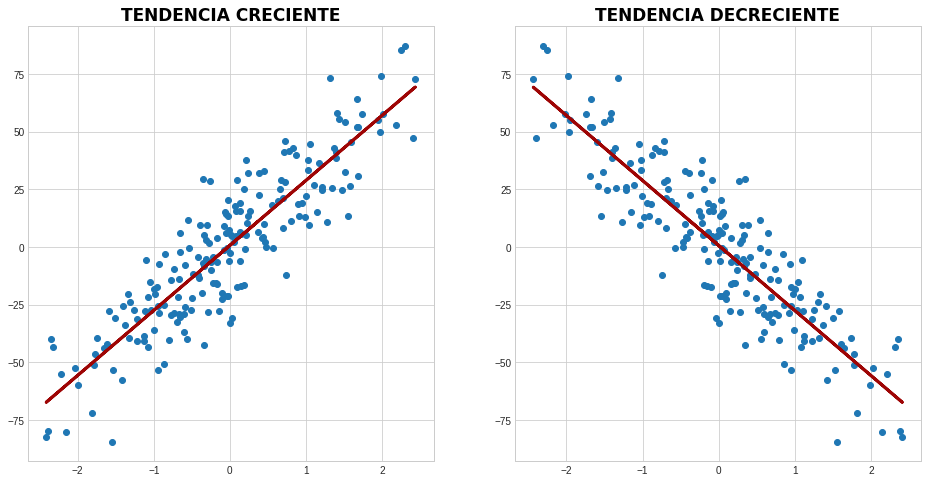
Un ejemplo de esto es lo que hace Excel para mostrar tendencias en los datos; para que te des una idea más detallada, aquí puedes ver cómo ellos mismos mencionan utilizar el método de mínimos cuadrados para sus fines: tendencias en Excel.
Con esto que hemos aprendido sobre la regresión lineal ya hemos obtenido un vasto panorama sobre cuál es su objetivo y cómo podemos utilizarla para solucionar problemas de ciencia de datos.
Ahora, antes de pasar a la práctica en Python, atendamos a sus definiciones matemáticas.
Definición matemática de la regresión lineal simple

Las definiciones matemáticas de la regresión lineal y el método de los mínimos cuadrados son relativamente sencillas, pero antes debemos asegurarnos de que tenemos bien presente lo básico respecto a las rectas y su interpretación en el espacio.
Echemos un vistazo a estos aspectos.
Ecuación de la recta e interpretación geométrica
Definición 3.2. (Ecuación de la recta). La ecuación de la recta es la expresión matemática que al ser evaluada/mapeada como una función describe la dirección y posición de una recta en un plano cartesiano. Su forma es la siguiente:
\begin{aligned}
y=mx+b\:, \tag{3.9}
\end{aligned}
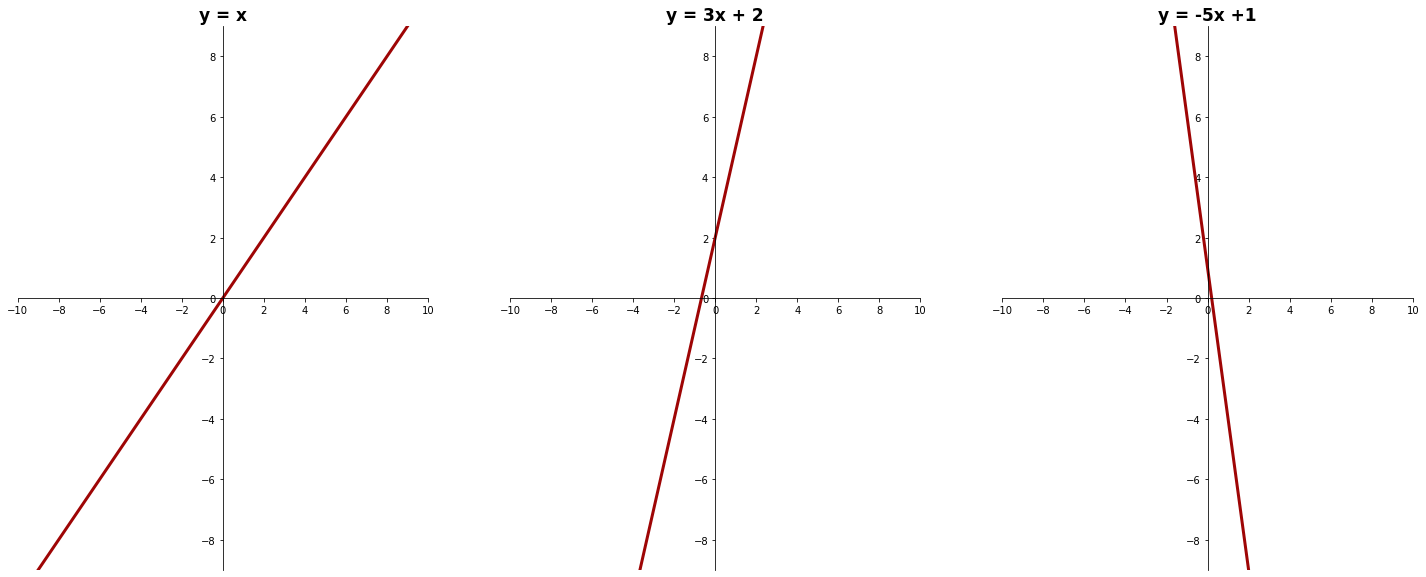
donde m \in \mathbb{R} es el valor de la pendiente (la cual determina su inclinación) y b\in \mathbb{R} es el valor en el que la recta se intersepta con el eje y. Se dice que m y b son sus parámetros o regresores.
En la Figura 3.2.7 se pueden visualizar diferentes ejemplos de cómo varía la presentación de la recta de acuerdo a diferentes variantes de sus parámetros:
Componente aleatorio
Como hemos comprobado tanto en el recorrido anterior como al inicio de este, la ecuación de una recta se puede utilizar para representar patrones en conjuntos de datos que consten de dos variables con una relación lineal entre estas.
En nuestro ejemplo sobre calificaciones, los puntajes obtenidos por los estudiantes dependen del número de horas que dedicaron al estudio. Al identificar visualmente una relación lineal en la Figura 3.2.1, se decidió que se podía utilizar una recta para modelar este patrón subyacente.
Por lo tanto, si suponemos que la interacción de este par de variables puede ser modelada por la ecuación de una recta, la variable independiente x representa a las horas de estudio, mientras que la variable dependiente y es la calificación obtenida (ya que los valores de esta última dependen de los valores de la otra).
Por razones de consistencia en nuestra notación matemática, reescribiremos la ecuación de la recta de la siguiente forma:
\begin{aligned}
y=\Theta_{0}+\Theta_{1}x\:, \tag{3.10}
\end{aligned}
donde y es la variable dependiente, y x la variable independiente parametrizada por \Theta, siendo \Theta_0 la intersección con las ordenadas (antes b), y \Theta_1 la pendiente de la recta (antes m).
Ahora que tenemos definida la forma de nuestra ecuación, y hemos identificado un posible patrón lineal en el comportamiento de los datos, notemos que la dispersión de estos no dibuja una línea recta exacta, sino que estos se distribuyen en una forma cercana a esta, como se puede constatar en la Figura 3.3.2.
Esto sucede porque no existe ningún fenómeno completamente determinista (hasta donde sabemos/creemos); siempre que tengamos un conjunto de datos de cualquier tipo, notaremos que no existe una relación completamente predecible entre las variables que lo componen (por ejemplo, no todos los alumnos que estudien 5 horas obtendrán siempre la misma calificación).
Se dice, entonces, que este tipo de fenómenos son de naturaleza probabilística, y por lo tanto, su comportamiento no puede ser descrito con total precisión por un modelo matemático. Por ello, cuando se intenta describir la relación entre variables asignadas a un conjunto de datos mediante una expresión matemática, se debe añadir un componente aleatorio que representa este «ruido» o aleatoriedad en las observaciones.
Tomando en cuenta estas consideraciones, redefinimos que la variable y se relaciona con la variable x a través de la ecuación:
\begin{aligned}
y=\Theta_{0}+\Theta_{1}x+\varepsilon\:, \tag{3.11}
\end{aligned}
donde \varepsilon es la variable que representa al componente aleatorio, el cual suele ser llamado error aleatorio.


Y de hecho, otro punto importante es que se asume que estas «desviaciones» tienen una distribución normal alrededor de la recta, es decir, su media cae sobre la recta, y los puntos más alejados de esta son poco comunes.

Puede llegar a ser poco intuitivo, pero con tenerlo presente basta. Para entender mejor los conceptos hasta aquí expuestos relacionados a la regresión lineal, y una parte de las bases de los objetivos del aprendizaje de máquinas, podemos resumir la lógica que precede al uso de la regresión lineal de la siguiente manera:
- Tenemos un conjunto de datos que consta de un par variables, de las cuales los valores de una dependen de la otra.
- Al explorarlo, determinamos que podemos modelar su comportamiento con la función de una recta.
- Ahora debemos obtener dicha función, por lo que para esto asumimos que existe tal modelo matemático.
- Habiendo asumiendo lo anterior, también se debe suponer que hay cierto ruido o componente aleatorio que genera puntos fuera de esa recta, entre los cuales estarán todas o una parte de las observaciones de las que consta el conjunto de datos, por lo que todo modelo obtenido no tendrá una capacidad predictiva totalmente exacta.
La cuestión clave a resolver ahora es: ¿cómo obtenemos dicha ecuación?
La regresión lineal como técnica de aprendizaje supervisado
Es aquí donde concebimos a la regresión lineal como la simiente de un modelo de machine learning. Recordemos que el aprendizaje supervisado tiene como objetivo encontrar, de entre un conjunto de hipótesis h(x), el modelo matemático que describa de forma más aproximada el comportamiento de un conjunto de datos, justo como reza la Definición 3.1 mostrada en nuestra última expedición.
Esto quiere decir que, ahora que sabemos que estamos buscando un patrón que puede ser representado por una recta, sabemos que existe un conjunto infinito de posibles rectas, y que entre estos debemos hallar el que se ajuste mejor a nuestros datos. Un ejemplo de esto lo podemos visualizar en la Figura 3.2.8:
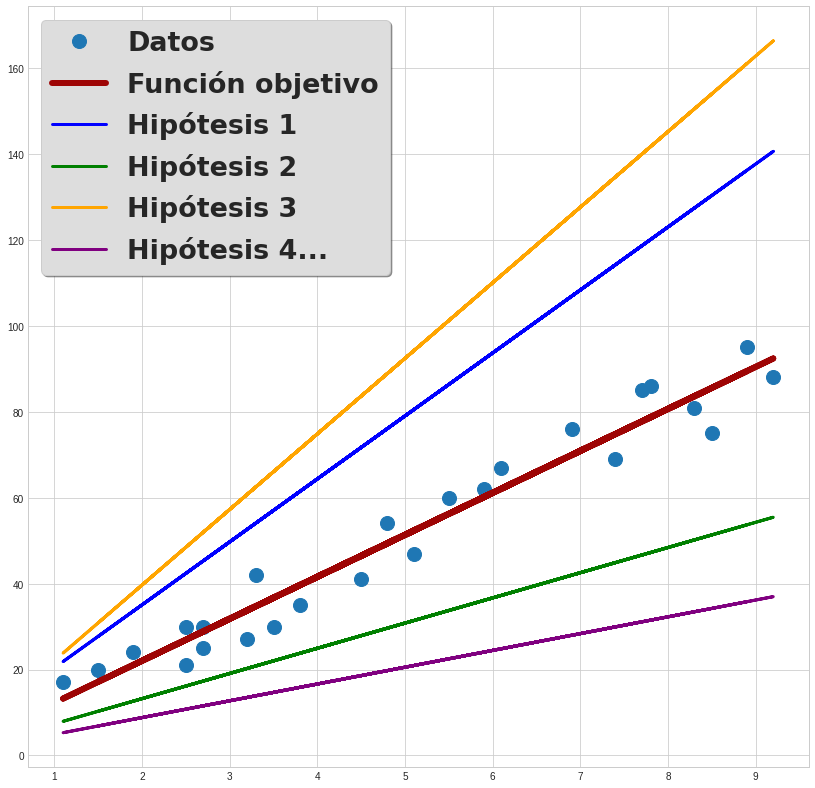
En esta ilustración se observa a un grupo de líneas dadas por funciones (hipótesis) con diferentes valores de sus parámetros, y la función objetivo, la cual es el modelo ideal que dibuja el patrón más afín a la dispersión de los datos.
Para ser más conscientes de cómo surgen estas rectas, recordemos que la función lineal ideal f(x), y la función lineal hipotética h(x), se expresan como sigue:
\begin{aligned}
f(x)=\Theta_{0}+\Theta_{1}x \tag{3.12}
\end{aligned}
\begin{aligned}
h(x)=\theta_{0}+\theta_{1}x\:, \tag{3.13}
\end{aligned}
Esta búsqueda de un modelo matemático entre posibles hipótesis a partir de datos etiquetados es lo que le confiere a la regresión lineal su puesto dentro de los anaqueles del aprendizaje supervisado, y por lo tanto, del aprendizaje automático.
Como ya he mencionado, la forma de obtener este modelo no es única, pero la más común es el método de mínimos cuadrados, el cual forma parte de un marco general del machine learning.
Minimización del riesgo empírico (empirical risk minimization), un enfoque general del aprendizaje de máquinas
La esencia del método de mínimos cuadrados reside en hallar la recta más cercana a las salidas del conjunto de datos. Para esto, lo que se hace es recurrir a un marco general del machine learning, el cual consiste en resolver el cómo seleccionar el modelo matemático más apropiado de entre el conjunto de hipótesis posibles.
¿Cómo lograrlo?, esto se puede lograr comparando las predicciones generadas por la hipótesis propuesta y los puntos que conforman al conjunto de datos.
Para observar este proceso, utilizaremos las funciones de las Ecuaciones (3.12) y (3.13) para calcular salidas o predicciones de una hipótesis en particular. Supongamos que nuestro modelo h_{\theta}(x) (hipótesis) para la estimación de datos sobre el conjunto de datos de calificaciones tiene la siguiente forma:
\begin{aligned}
h(x)=3+10x,\: \tag{3.14}
\end{aligned}
con \theta_{0}=3 y \theta_{1}=10.
Esta función puede utilizarse para predecir cuál es el valor del puntaje de un alumno dadas determinadas horas de estudio, por lo que la usaremos para estimar el valor del puntaje en 4.5 horas:
\begin{aligned}
h(4.5)=3+10(45)=48.\: \tag{3.15}
\end{aligned}
Esto quiere decir que el modelo calcula que para 4.5 horas de estudio, un alumno obtendrá aproximadamente un 48 de calificación.
Revisando el conjunto de datos (Tabla 3.2.1), podemos constatar en el renglón número 12 (doceavo ejemplo de entrenamiento) que el valor observado para este valor es de 41, por lo que la diferencia entre este y la cantidad real (asumiendo que está dada por la función objetivo y = f(x)) es:
\begin{aligned}
\hat{y}_{12}-y_{12}&=48-41\\
&=7, \tag{3.16}
\end{aligned}
donde \hat{y}_n representa al valor obtenido al evaluar la función hipotética en 4.5, como se hizo en (3.15).
Esta diferencia entre valores correspondientes al conjunto de datos y valores predichos por el modelo, es lo que se conoce como «error» o «riesgo«, y mientras este es más pequeño, el modelo es mejor en sus predicciones, ya que esto significa que sus salidas se asemejan más a las cantidades reales.
Dado esto, es lógico pensar que, para obtener el mejor modelo, las diferencias entre los puntos predichos por el modelo y los puntos pertenecientes al conjunto de datos debe ser la menor posible.
La operación de minimizar estas diferencias o errores es lo que se conoce como minimización del riesgo empírico, y es un marco general a través del cual se puede abordar la obtención de modelos de machine learning.
Regresión lineal simple
Definición 3.2. (Regresión lineal simple). La regresión lineal simple es un método cuyo objetivo es encontrar la ecuación que describe la relación lineal entre una variable independiente x, una variable dependiente y, y un componente aleatorio \varepsilon. La ecuación resultante tiene la forma
\begin{aligned}
y=\Theta_{0}+\Theta_{1}x+\varepsilon\:, \tag{3.17}
\end{aligned}
donde \Theta_{0} y \Theta_{1} son los regresores que la parametrizan.
Función de error para la regresión lineal
Como lo determina la minimización del error empírico, para evaluar qué tan bien predice valores el modelo hallado por la regresión lineal, se comparan las salidas de este con los valores del conjunto de datos (también conocido como el terreno verdadero, terreno real, o verdad fundamental).
Definición 3.3 (Error). Dado un conjunto \mathcal{D}=\lbrace (x_{1},y_{1}),…,(x_{n},y_{n}),…,(x_{N},y_{N})\rbrace de N datos etiquetados, una función hipótesis h(x) =\theta_{0}+\theta_{1}x ajustada a los datos, donde \hat{y}_n es la salida de la hipótesis evaluada en x_{n}, y y_{n} la n-ésima salida del conjunto de datos, el n-ésimo error e_{n} está dado por
\begin{aligned}
e_{n}=y_{n}-\hat{y}_n\:, \tag{3.18}
\end{aligned}
la cual es la diferencia entre las salidas del conjunto de datos, y las salidas generadas por h(x).
Teniendo esto en cuenta, finalmente definimos la función de error, o función de pérdida para la regresión lineal.
Definición 3.4 (Función de error cuadrático medio). La función de error para la regresión lineal es la función de error cuadrático, la cual tiene la forma
\begin{aligned}
&l(y_{n},\hat{y}_n)=e_{n}^{2} \tag{3.19}\\
&l(y_{n},\hat{y}_n)=(y_{n}-\hat{y}_n)^{2}.
\end{aligned}
Esta función calcula el cuadrado de los residuales, es decir, el cuadrado de las diferencias entre lo que predice el modelo y los valores del conjunto de datos. Lo que buscaremos ahora será minimizar esos errores con la función del error cuadrático medio:
\begin{aligned}
\text{MSE} &= \min \frac{1}{N} \sum_{n=1}^{N} l(y_n, \hat{y}_n) \tag{3.20} \\
&= \min \frac{1}{N} \sum_{n=1}^{N} (y_n - \hat{y}_n)^2,
\end{aligned}
la cual minimiza la suma del cuadrado de las diferencias entre las predicciones de \hat{y}_n y las salidas y_{n} del conjunto de datos.
Esta minimización implica que se encontrarán los parámetros \theta_{0} y \theta_{1} que reduzcan las diferencias entre las predicciones del modelo y los valores reales.
Haciendo predicciones con el modelo ajustado
El desarrollo matemático correspondiente a la obtención de las ecuaciones que determinan los valores de los regresores \theta_{0} y \theta_{1} que minimizan la función MSE (del error cuadrático medio, por sus siglas en inglés: mean squared error) no serán mostradas aquí para evitar alargar demasiado el recorrido.
Sin embargo, si se desea explorar esta parte, recomiendo el capítulo 11 del libro Probabilidad y estadística de Walpole, o este texto del profesor Esteban Hurtado de la facultad de ciencias de la UNAM: El método de mínimos cuadrados.
Para finalizar, haremos algunas estimaciones con la función encontrada por la regresión lineal.
Supongamos que hemos calculado los parámetros de la ecuación de la recta utilizando el método de mínimos cuadrados, y hemos obtenido la siguiente función:
\begin{aligned}
h(x)=2.48+9.77x\:, \tag{3.21}
\end{aligned}
donde \theta_{0}=2.48 y \theta_{1}=9.77.
Ahora lo que buscamos es obtener alguna aproximación de una calificación dada un número de horas que no se encuentre dentro de nuestro conjunto de datos. En esta ocasión, elegiremos el 5.3.
Sustituimos en (3.21):
\begin{aligned}
h(x)=2.48+9.77(5.3)=54.26.\: \tag{3.22}
\end{aligned}
Por lo tanto, nuestro modelo estima una calificación de aproximadamente 54 para alumnos que estudien 5.3 horas, lo cual es consistente con los valores de la Tabla 3.2.1.
En la Figura 3.2.9 se ilustra el resultado:
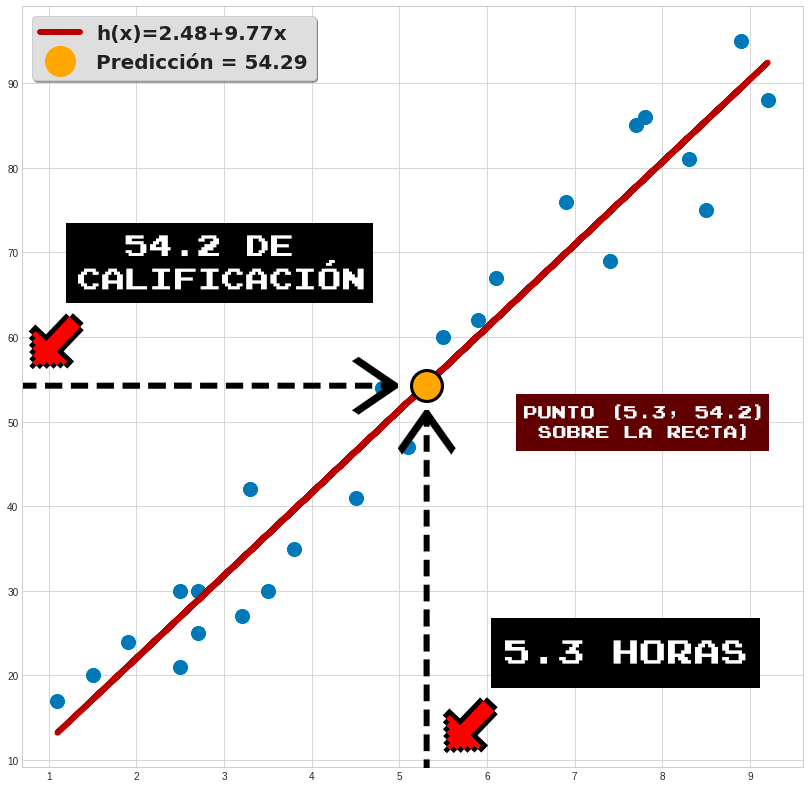

Para esos casos aún se puede utilizar la regresión lineal, pero en su versión multivariable. Lo definiremos a continuación, pero de manera opcional (este recorrido ha sido exaustivo). Ya luego la retomaremos.
Regresión lineal multivariable (opcional)
Es importante que al menos sepas que existe una versión de la regresión lineal que considera a más de una variable independiente. Esta se llama regresión lineal multivariada o multivariable, y te puede llegar a ser de utilidad.
Definición 3.5 (Regresión lineal multivariable). La regresión multivariable es un método cuyo objetivo es encontrar la ecuación que describe la relación lineal entre varias variables independientes x_1, x_2, \dots, x_n , una variable dependiente y , y un componente aleatorio \varepsilon . La ecuación resultante tiene la forma
y = \Theta_0 + \Theta_1 x_1 + \Theta_2 x_2 + \dots + \Theta_n x_n + \varepsilon, \tag{3.22.1}donde \Theta_0, \Theta_1, \dots, \Theta_n son los regresores que la parametrizan.
Esto quiere decir que, en caso de existir, puedes modelar la relación de más de una variable de entrada con tu salida. Por ejemplo, se podrían utilizar las variables número de horas de estudio, edad del alumno, y nivel socioeconómico del alumno para estimar la calificación total que obtendrá un estudiante, lo cual generaría una ecuación como la que sigue:
y = \Theta_0 + \Theta_1 x_1 + \Theta_2 x_2 +\Theta_3 x_3, \tag{3.22.2}donde
- x_1= horas de estudio
- x_2= edad
- x_3= nivel socioeconómico
Supuestos de la regresión lineal (opcional)
Para cerrar esta sección, haré mención de los supuestos de la regresión lineal, los cuales son asunciones que deben de cumplirse para que la técnica pueda ser correctamente aplicada. Esto es importante para determinar si el patrón de la relación entre variables de un conjunto de datos puede ser eficientemente modelado por una regresión lineal, y aunque no las estudiaremos a profundidad, al menos es importante que sepas de su existencia.
Si no los entiendes a la perfección, no te preocupes; si deseas aprenderlo más a fondo, recomiendo el capítulo 5.1 del libro Interpretable Machine Learning de Christopher Molnar.
Supuestos de la regresión lineal:
- Linealidad: se asume que las variables involucradas guardan relaciones lineales entre sí, es decir, la ecuación que las modela son el resultado de una combinación lineal de la variable independiente y los residuos (componente aleatorio).
- Homocedasticidad: la varianza de los errores es constante.
- Independencia: las observaciones son independientes una de la otra.
- Normalidad: la variable dependiente posee una distribución normal.
- No-colinealidad: no existe relación lineal exacta entre ninguna de las variables independientes.
- Exogeneidad: las variables independientes no deben estar correlacionadas con los términos de error. Esto significa que las variables predictoras son exógenas, es decir, cualquier cambio en las variables independientes no debe estar relacionado con el término de error de la regresión.

Regresión lineal simple: código de programación en python

Hemos llegado al final de esta travesía. Como último paraje a recorrer, confrontaremos una situación en la que haremos uso de la regresión lineal simple en Python para la solución de un problema. Para este caso, proseguiremos con el tema de automóviles y sus características con el fin de dar continuidad a lo visto en la introducción al preprocesamiento de datos, para lo cual utilizaremos un conjunto de datos diferente y más actualizado.
Da clic aquí para dirigirte a la práctica en Colab:

También puedes observar el código en la siguiente ventana, pero sin posibilidad de ejecutarlo:
Aquí finaliza nuestra travesía. Por fin has aprendido sobre el funcionamiento y uso de un algoritmo de machine learning, y lo has puesto en acción. En la siguiente exploración conocerás a la afamada regresión logística, un método que se enfoca en tareas de clasificación, y el cual también se considera clave para el estudio de modelos más avanzados.