Si has entrenado un modelo de clasificación utilizando técnicas de aprendizaje de máquinas (por ejemplo, ajustando un modelo mediante una regresión logística), debes evaluar qué tan bueno es haciendo su trabajo. Esto se logra mediante el uso de diferentes métricas que derivan de la comparación entre las clasificaciones generadas con el modelo y valores pertenencientes a un cojunto de datos de prueba.

Justo como hicimos cuando aprendimos sobre métricas para medir el desempeño de modelos de regresión, en esta sesión revisaremos qué metricas cumplen con este objetivo para modelos que categorizan datos, cómo se usan, analizan, e interpretan; todo llevado a la práctica en un caso utilizando Python.

Inventario recomendado

Matemáticas: algo de álgebra, probabilidad y estadística

Fundamentos del aprendizaje supervisado

Regresión logística

Función de pérdida de la regresión logística

Google Colab

Programación en Python

Algún aperitivo

Métricas de evaluación de modelos de clasificación: cuáles y cómo utilizarlas

Recordemos que en aprendizaje supervisado podemos atacar dos tipos de enfoques en cuanto a objetivos de modelos: modelos de regresión y modelos de clasificación.

Donde los modelos de regresión predicen valores de una variable continua (salida) respecto a los valores de variables con las que está relacionada (entradas). De este tipo de modelos ya hemos trazado cómo evaluar su desempeño al generar predicciones sobre datos nuevos no pertenecientes al conjunto de datos de entrenamiento.

Los modelos de clasificación, por otro lado, tratan sobre funciones que, mediante un análisis de probabilidades, determinan a qué clase pertenece cada dato de entrada de entre un grupo de categorías predefinidas.

Un ejemplo de esto es el caso que hemos desarrollado en la práctica de Python de la regresión logística, en la que se clasificaron canciones de entrada en géneros músicales de acuerdo a sus características. Más adelante veremos cómo utilizar esas mismas clasificaciones para evaluar los modelos con Python, pero hoy trabajaremos con un nuevo ejemplo para explicar cómo determinar las capacidades de clasificación de un modelo de este tipo, las cuales no contemplan ninguna de las métricas vistas en la anterior exploración.

Métricas para evaluar modelos de clasificación

Antes de exponer un nuevo ejemplo, haré mención de las métricas de las que puedes disponer para evaluar modelos de clasificación. Primero, y por que ya las hemos mencionado y estudiado con anterioridad, puedes considerar el uso de funciones de pérdida.

Las funciones de pérdida más comunes para modelos de clasificación son las siguientes:

• Pérdida de entropía cruzada (Cross Entropy Loss).
• Pérdida de entropía cruzada sigmoidea (Sigmoid Cross Entropy Loss).
• Pérdida de entropía cruzada softmax (Softmax Cross Entropy Loss).
• Verosimilitud logarítmica negativa (Negative Log-Likelihood).
• Pérdida 0-1 (0-1 Loss).
• Pérdida de Hinge (Hinge Loss).
• Pérdida Huber modificada (Modified Huber Loss).
• Pérdida de Hinge suavizada (Smooth Hinge Loss).
• Pérdida de Hinge reescalada (Rescaled Hinge Loss).
• Pérdida de rampa (Ramp Loss).
• Error de clasificación mínimo (Minimum Classification Error).
• Pérdida logarítmica (Log Loss).
• Pérdida exponencial (Exponential Loss).
• Pérdida basada en margen (Margin-Based Loss).
• Ranqueo por parejas (Pairwise Ranking).
• Ranqueo por tripleta (Triplet Ranking).
• Pérdida contrastiva (Contrastive Loss).
• Pérdida pinball (Pinball Loss).
• Pérdida pinball truncada (Truncated Pinball Loss).

No, siendo honestos dudo que haya alguien que las conozca y haya aplicado todas, salvo quienes se hayan dedicado específicamente a escribir artículos científicos sobre funciones de pérdida de modelos de clasificación. Solo lo pongo aquí para que sepan que existen.

Mientras menos ignoremos sobre lo que nos especializamos, mejor. Además, deben tener en cuenta que las funciones de pérdida tienen un amplio uso en el entrenamiento de modelos, más que en su evaluación final. Para eso, suelen utilizarse otras métricas, que son las que veremos a continuación.

Además de las funciones de pérdida, entre las cuales ya estudiamos con gran detalle la entropía cruzada, se cuenta con métricas que son mucho más frecuentes en la práctica de la ciencia datos.

Todas estas parten de la organización de los resultados en algo que se conoce como matriz de confusión. Es un concepto clave en ciencia de datos que debemos conocer.

Matriz de confusión para evaluar modelos de clasificación

La matriz de confusión es una herramienta típica para la evaluación de modelos que realizan clasificaciones binarias. De forma más específica, la matriz de confusión es una matriz de dos dimensiones utilizada para evaluar sistemas de clasificación mostrando la cantidad de datos correcta e incorrectamente categorizados.

Vamos a revisar con detalle cómo luce y cómo se utiliza, pero para entenderla de forma concreta, antes debemos definir los elementos que la componen.

Componentes de la matriz de confusión

Una matriz de confusión está conformada por los valores de las clasificaciones binarias (de dos clases) realizadas por un modelo entrenado. Se distinguen dos tipos:

• El modelo predice que un dato pertenece a la clase 0 (que también llamaremos clase <<negativa>>).
• El modelo predice que un dato pertenece a la clase 1 (que también llamaremos clase <<positiva>>).

Teniendo esto en cuenta, en la matriz de confusión se utilizan este par de clasificaciones y se dibujan los siguientes casos de acuerdo a los aciertos o errores del modelo:

• El modelo predice que un dato pertenece a una clase 1 (positiva), y su predicción es correcta.
• El modelo predice que un dato pertenece a una clase 1 (positiva), pero en realidad pertenece a la clase 0 (negativa), por lo que su predicción es incorrecta.
• El modelo predice que un dato pertenece a una clase 0 (negativa), y su predicción es correcta.
• El modelo predice que un dato pertenece a una clase 0 (negativa), pero en realidad pertenece a la clase 1 (positiva), por lo que su predicción es incorrecta.

Así es, y cada uno de estos casos tiene un nombre, vamos a revisarlos, definirlos, y compararlos con ejemplos.

Ejemplo de evaluación de modelo clasificación con matriz de confusión

Para el estudio de la matriz de confusión, vamos a plantear un caso típico en el que entrenamos un modelo para clasificar reseñas de películas en <<positivas>> y <<negativas>>.

Las entradas del modelo (el conjunto de datos) son reseñas de películas, por ejemplo:

Esta es una reseña de película que se considera positiva, ya que elogia a la obra.

Sin embargo, podemos tener entradas de este otro tipo:

En esta otra reseña podemos notar una intención comunicativa diferente, en la que la película no es del agrado del crítico, y por lo tanto se considera negativa.

El objetivo de utilizar un algoritmo de aprendizaje automático para procesar esta información, es entrenar un modelo que, dada una nueva reseña, la clasifique como positiva o negativa.

Por ahora necesito saber, con los conocimientos que tenemos hasta esta parte de nuestras exploraciones, ¿qué tanto me puedes decir sobre esta tarea de ciencia de datos?

Entonces, podemos distinguir los siguientes elementos en este proyecto de machine learning:

• Conjunto de datos: está compuesto por reseñas positivas y negativas de películas . Los datos son fragmentos de texto, por lo que son datos no estructurados, de tipo cualitativo. Además, los datos están etiquetados, señalando cuáles reseñas son positivas y cuáles negativas.
• Objetivo: entrenar un modelo de machine learning que clasifique reseñas en positivas o negativas.
• Algoritmo a utilizar: algún algoritmo de aprendizaje supervisado de clasificación, como la regresión logística.

Ahora que conocemos el caso de estudio, prosigamos con la definición de los componentes de la matriz de confusión.

Tipos de falsos y verdaderos de la matriz de confusión

Revisemos ahora los casos que se toman en cuenta en una matriz de confusión y dan vida a las métricas para evaluar modelos de clasificación.

Verdadero Positivo (VP)

Un verdadero positivo es una entrada que el modelo ha clasificado correctamente como positiva.

Nuestro modelo de clasificación de reseñas de películas se ha entrenado determinando que la clase positiva es 1, por lo tanto, un verdadero positivo significa que se ha entregado al modelo una reseña positiva y este la ha clasificado correctamente en esta categoría.

Verdadero Negativo (VN)

Un verdadero negativo es una entrada que el modelo ha clasificado correctamente como negativa.

Dado que la clase negativa es 0, un verdadero negativo generado por el modelo de clasificación de reseñas sucede cuando se le entrega una reseña negativa y la clasifica correctamente.

Falso Positivo (FP)

Un falso positivo es un caso en el que modelo clasifica incorrectamente una entrada que pertenece a la clase negativa. En estadística también se le conoce como error Tipo I.

En nuestro ejemplo, un falso positivo se da cuando se le entrega al modelo clasificador una reseña negativa, y este la categoriza como reseña positiva.

Falso Negativo (FN)

Un falso negativo se da cuando el modelo ha clasificado de forma errónea una entrada que es de la clase positiva, asignándola como negativo. En estadística también se le conoce como error Tipo II.

En nuestro ejemplo, un falso negativo se da cuando se le entrega al modelo clasificador una reseña positiva, y este la categoriza como reseña negativa.

Estos son los diferentes casos que componen a la matriz de confusión, los verdaderos positivos y negativos (VP y VN) y los falsos positivos y negativos (FP Y FN) son lo que se utilizan para obtener métricas de evaluación de modelos de clasificación.

Volvamos a la matriz de confusión.

Estructura de la Matriz de Confusión

La matriz de confusión es una herramienta para la evaluación de modelos de clasificación organizando la cantidad de clasificaciones binarias correctas e incorrectas en una matriz de dos dimensiones, como se muestra en la Figura 3.7.3:

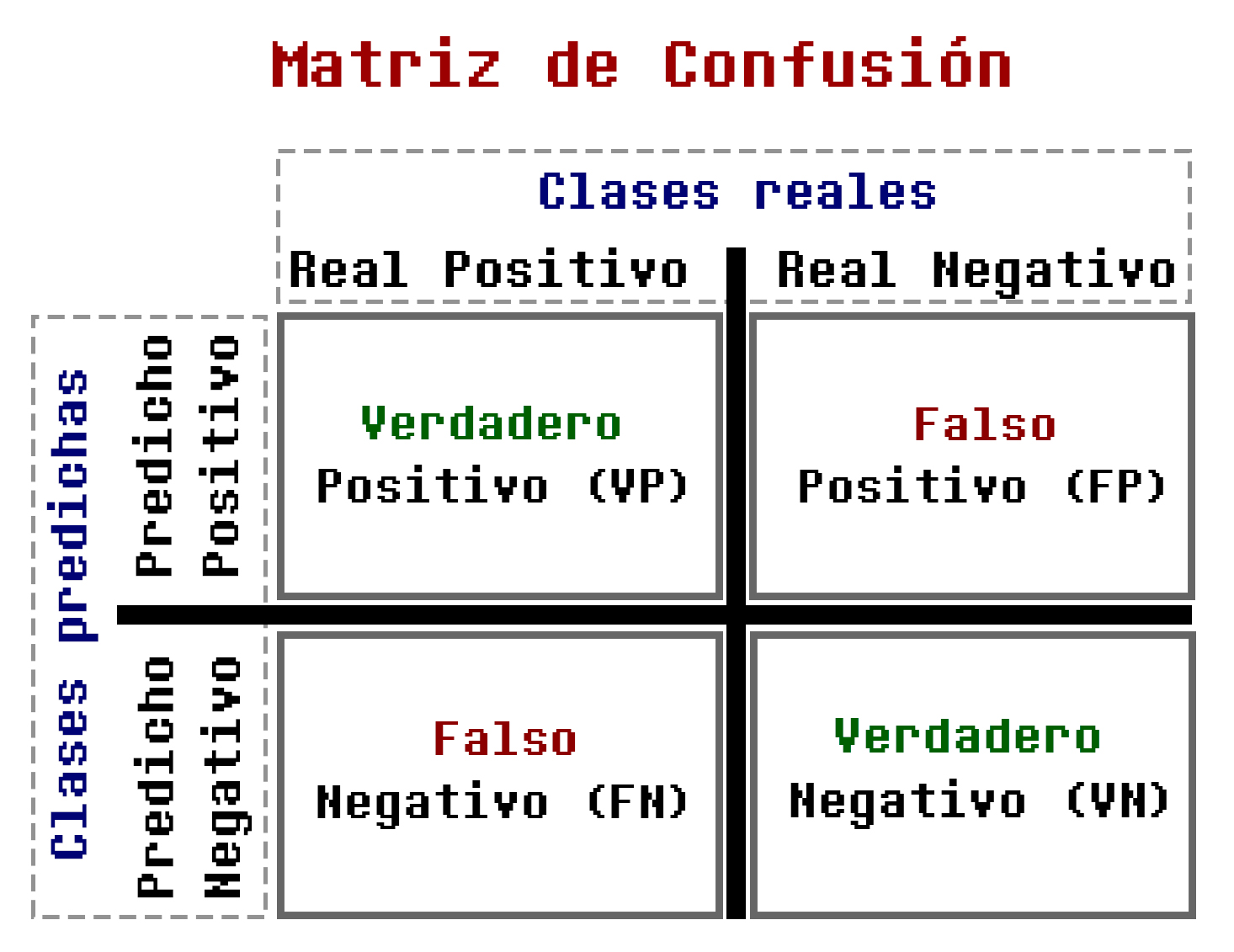
Donde, como ya vimos antes:

• VN y VP son verdaderos positivos y negativos, ese decir, las clasificaciones realizadas correctamente.
• FN y FP son falsos positivos y negativos, ese decir, las clasificaciones realizadas incorrectamente.
• Nótese que la diagonal de la matriz (VN y VP) muestra las predicciones correctas.
• De forma inversa, los elementos fuera de la diagonal (FP y FN) muestran las predicciones incorrectas.

Con esto debería quedar claro cómo está compuesta una matriz de confusión. Se trata simplemente del arreglo de los resultados de utilizar el modelo de clasificación en el conjunto de datos de prueba: se registran los errores y aciertos, y se categorizan como verdaderos o falsos respecto a cada clase (como es clasificación binaria, estas se consideran como negativa y positiva).

Por fin podemos hablar de las métricas que se derivan de estos valores.

Utilizando los resultados de una matriz de confusión, se pueden derivar las siguientes medidas para evaluar modelos de clasificación:

• Exactitud (Accuracy).
• Precisión (Precision).
• Sensibilidad (Recall, Sensitivity).
• Puntaje F1 (F1 Score).
• Curvas ROC y AUC.
• Tasa de falsos positivos (False Positive Rate).
• Tasa de falsos negativos (False Negative Rate).
• Tasa de falsas omisiones (False Omission Rate).
• Prevalencia (Prevalence).
• Valor predictivo negativo (Negative Predictive Value).
• Marcación (Markedness).
• Razón de probabilidades diagnóstica (Diagnostic Odds Ratio).
• Coeficiente de correlación de Matthews (Matthews Correlation Coefficient).
• Puntuación de amenaza, índice de éxito crítico, índice de Jaccard (Threat Score, Critical Success Index, Jaccard Index).
• Umbral de prevalencia (Prevalence Threshold).
• Exactitud balanceada (Balanced Accuracy).
• Índice de Fowlkes-Mallows (Fowlkes-Mallows Index).
• Razón de verosimilitud positiva (Positive Likelihood Ratio).
• Razón de verosimilitud negativa (Negative Likelihood Ratio).
• Información (Informedness).

Si te preguntas cómo es que se obtienen estas métricas de una matriz de confusión, lo veremos más adelante en esta exploración.

Sí, son demasiadas, pero de entre estas se suelen usar solo un subconjunto relativamente pequeño.

Estas son las métricas de evaluación de modelos de clasificación más utilizadas:

• Exactitud.
• Precisión.
• Sensibilidad.
• Puntaje F1.
• Pérdida de entropía cruzada.

Y con esto llegamos a las medidas que estaremos conociendo y poniendo a prueba aquí. Tenemos cuatro métricas derivadas de la matriz de confusión, y una obtenida por función de pérdida (entropía cruzada). Estas son de bastante utilidad para la evaluación de modelos de clasificación.

Para entenderlo mejor, lo desarrollaremos y veremos aplicado a nuestro caso de estudio de clasificación de reseñas.

Ejemplo de evaluación de modelo de machine learning con métricas de la matriz de confusión

Supondremos que hemos entrenado un modelo de aprendizaje supervisado para la categorización de reseñas de películas, y lo hemos utilizado sobre un conjunto de datos de prueba, donde obtuvimos los siguientes resultados:

• Verdaderos Positivos (VP): 90 reseñas positivas fueron clasificadas correctamente como positivas.
• Verdaderos Negativos (VN): 80 reseñas negativas fueron clasificadas correctamente como negativas.
• Falsos Positivos (FP): 20 reseñas negativas fueron clasificadas incorrectamente como positivas.
• Falsos Negativos (FN): 10 reseñas positivas fueron clasificadas incorrectamente como negativas.

Ahora organizamos esta información en la matriz de confusión:

Compara esta matriz con la de la imagen Figura 3.7.3 y podrás notar cómo es que se han realizado los acomodos de las cifras obtenidas.

Métricas Derivadas de la Matriz de Confusión

Con lo que hemos visto hasta ahora basta para poder aprender sobre métricas de evaluación de modelos de clasificación, para lo cual se utilizan los valores organizados en la matriz de confusión, y se calculan mediante fórmulas sencillas.

Exactitud (Accuracy)

La exactitud es una métrica que mide la proporción de clasificaciones correctas entre todas las clasificaciones realizadas. Se calcula con la siguiente fórmula:

\text{Exactitud} = \frac{VP + VN}{VP + VN + FP + FN}, \tag{3.69}

donde VP, VN, FP y FN son los valores de la matriz de confusión revisados en la sección anterior. Esta fórmula es bastante simple, consiste en sumar las predicciones correctas (VP y VN) y dividirlas entre todas las demás, por lo que arroja una proporción de los datos correctamente clasificados por el modelo.

Aquí haremos una breve pausa para revisar un término de importancia medular. Para interpretar correctamente esta métrica y las subsecuentes, debemos tener en cuenta un tipo de estructura que puede presentar un conjunto de datos: datos desbalanceados.

Datos desbalanceados

Los datos desbalanceados es una propiedad de un cojunto de datos en el que las categorías (datos de salida objetivo para el entrenamiento de un modelo de clasificación) no están repartidas de manera equitativa. Esto significa que una o más clases tienen significativamente más ejemplos de entrenamiento que otras.

Para ilustrarlo, recordemos que tenemos datos etiquetados, donde, en el caso de las tareas de clasificación, se designan clases a cada uno de los ejemplos de entrenamiento. Sin embargo, estos datos pueden llegar a estar desproporcionados (desbalanceados). Un ejemplo se puede observar en la Figura 3.7.4:

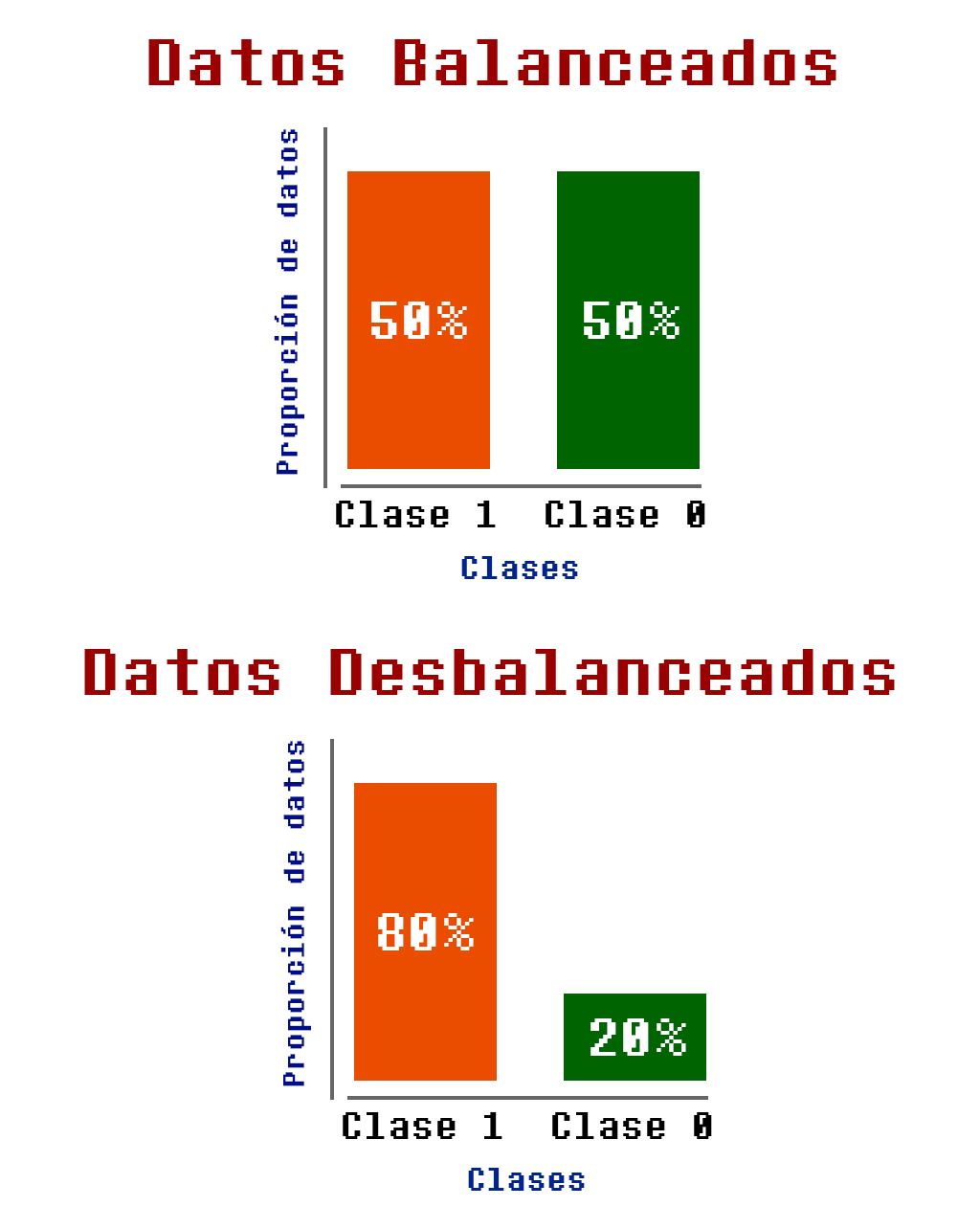
Pongamos otro ejemplo: se podrían tener 200 datos etiquetados con la clase 1, y solo 10 datos etiquetados con la clase 0. Esto significa que no se tiene una proporción igual entre datos que pertenecen a ambas clases (5% de los datos de una clase, y 95% de otra clase).

Esto puede llegar a generar confusión, ya que un modelo podría acertar en predecir todas las clases de tipo 1 y fallar en todas las clases de tipo 0, pero aún así, si calculamos su exactitud como se hace en la Ecuación (3.69), su precisión sería del 95%, porque las clases están desbalanceadas. Sin embargo, como en realidad no ha logrado clasificar correctamente ningún dato en la clase 0, se podría concluir que en realidad es 50% efectiva, lo cual lo hace un modelo poco eficiente.

Este tema de datos desbalanceados es algo que se debe tener en cuenta al evaluar modelos de clasificación. En una ocasión futura, veremos técnicas para lidear con esto desde el preprocesamiento de datos.

Interpretación de la exactitud

Ahora sí, volvamos con la métrica de Exactitud, y expliquemos como se interpreta. Esta mide la proporción de predicciones correctas realizadas por un modelo en relación con el total de predicciones. Es decir, evalúa qué tan bien el modelo clasificó correctamente tanto los casos positivos como los negativos en un conjunto de datos.

Los resultados de esta métrica se interpretan como sigue:

• Exactitud alta (valores cercanos a 1): Indican que el modelo tuvo un alto porcentaje de predicciones correctas.
• Exactitud baja (valores cercanos a 0): Indican un bajo desempeño del modelo, es decir, muchas predicciones incorrectas.

Limitaciones en cuanto a datos desbalanceados:

• En conjuntos de datos con clases desbalanceadas (por ejemplo, como ya hemos visto, donde los datos positivos son muy pocos en comparación con los negativos), la exactitud puede ser engañosa. Un modelo podría obtener una alta exactitud simplemente prediciendo siempre la clase con mayor predominancia. En estos casos, es mejor considerar métricas adicionales como la precisión, la sensibilidad (recall) o la métrica F1, que veremos a continuación.

Ejemplo de cálculo e interpretación de la exactitud

Ahora calcularemos la exactitud del modelo clasificador de reseñas. De acuerdo a los valores de la matriz mostrados en la Tabla 3.7.1 y a la fórmula de la Ecuación (3.69), se calcula como sigue.

\text{Exactitud} = \frac{VP + VN}{VP + VN + FP + FN} = \frac{90 + 80}{90 + 80 + 20 + 10} = \frac{170}{200} = 0.85 \tag{3.70}

Estos implica que el modelo tiene una exactitud del 85%, es decir, el modelo clasifica correctamente el 85% de las reseñas de películas. Es una buena métrica general, pero puede ser engañosa si las clases están desbalanceadas (no es el caso en nuestro ejemplo).

Precisión (Precision)

La precisión es una métrica que mide la proporción de clasificaciones de la clase positiva que se han hecho correctamente entre todos los datos pertenecientes a la clase positiva. Se calcula con la siguiente fórmula:

\text{Precisión} = \frac{VP}{VP + FP}. \tag{3.71}

Nótese que esta fórmula solo considera los positivos, tanto los aciertos como los errores. Quiere decir que refleja el porcentaje de datos correctamente clasificados para la clase 1 (positiva).

Interpretación de la precisión

Los resultados de la precisión se interpretan de la siguiente manera:

• Precisión alta (valores cercanos a 1): Significa que la mayoría de las predicciones positivas del modelo son correctas. Es decir, el modelo tiene pocos falsos positivos. Es importante en escenarios donde los falsos positivos son costosos o críticos, como en el diagnóstico médico.
• Precisión baja (valores cercanos a 0): Indica que el modelo realiza muchas predicciones positivas incorrectas, lo que sugiere un número elevado de falsos positivos.

Cálculo e interpretación en el ejemplo propuesto

Calcularemos la precisión del modelo clasificador de reseñas:

\text{Precisión} = \frac{VP}{VP + FP} = \frac{90}{90 + 20} = \frac{90}{110} \approx 0.818 \tag{3.72}

La precisión es aproximadamente 81.8%, lo que significa que de todas las reseñas clasificadas como positivas, el 81.8% realmente son positivas.

Sensibilidad o Exhaustividad (Recall)

La sensibilidad o exhaustividad es una métrica que mide el porcentaje de casos positivos correctamente identificados como positivos, considerando también aquellos positivos mal clasificados. Se calcula con la siguiente fórmula:

\text{Sensibilidad} = \frac{VP}{VP + FN} \tag{3.73}

Esta fórmula se diferencia de la precisión porque considera a los falsos negativos (FN), lo cual sucede porque su objetivo principal es medir la capacidad del modelo para identificar correctamente los casos positivos. Los falsos negativos representan los casos positivos que el modelo no logró detectar, por lo que son fundamentales para evaluar esta métrica. Si el modelo tiene un número alto de falsos negativos, significa que está fallando en detectar una gran cantidad de casos positivos. Esto reduce el valor de la Exhaustividad, indicando un desempeño deficiente en la detección de la clase positiva.

Interpretación de la sensibilidad

Los resultados de la sensibilidad se interpretan de la siguiente manera:

• Exhaustividad alta (valores cercanos a 1): El modelo es muy efectivo detectando los casos positivos. Es decir, tiene pocos falsos negativos. Esta métrica es ideal en escenarios donde es crucial no pasar por alto falsos negativos.
• Exhaustividad baja (valores cercanos a 0): Indica que el modelo falla al identificar muchos casos positivos, generando un alto número de falsos negativos.

Cálculo e interpretación en el ejemplo propuesto

Calcularemos la sensibilidad del modelo clasificador de reseñas:

\text{Sensibilidad} = \frac{VP}{VP + FN} = \frac{90}{90 + 10} = \frac{90}{100} = 0.9
 \tag{3.74}

La sensibilidad obtenida es del 90%, lo que indica que nuestro modelo detecta correctamente el 90% de las reseñas positivas. Esta métrica es útil cuando queremos reducir los falsos negativos, priorizando que la mayoría de las reseñas positivas se clasifiquen correctamente.

Casi, pero tienen una pequeña/gran diferencia. Creo que esto se puede prestar a malinterpretaciones, así que revisemos con un poco más de detalle.

Diferencia entre Precisión (precision) y Sensibilidad (recall) | Opcional

La precisión y la sensibilidad son métricas que calculan proporciones de verdaderos positivos, pero no sobre el mismo grupo de información. Considérese lo siguiente:

• La precisión se obtiene dividiendo los verdaderos positivos entre la suma de verdaderos positivos y falsos positivos (Ecuación 3.71). Recordemos que un falso positivo es un predicción errónea, lo cual significa que es un valor de la clase negativa (el modelo la asignó a la clase positiva, pero no acertó). Esto quiere decir que la precisión está obteniendo el porcentaje de predicciones correctas de la clase positiva entre las predicciones correctas e incorrectas de verdaderos positivos. Por lo tanto, un alto valor de precisión indica que el valor de los falsos positivos es bajo, y el modelo está clasificando datos correctamente en la clase positiva, entre otras palabras: de todas las predicciones positivas que hizo el modelo, cuántas son correctas.
• Por otro lado, la sensibilidad es la proporción de verdaderos positivos entre la suma de verdaderos positivos y falsos negativos (Ecuación 3.73). Los falsos negativos son valores que el modelo clasificó incorrectamente, que en realidad eran positivos pero se clasificaron como negativos. Esto significa que la sensibilidad toma en cuenta no solo los datos que el modelo asignó a la clase positiva, sino también los positivos que quedaron asignados a la clasificación incorrecta. Esto se traduce en que se calcula cuántos datos de la clase positiva fueron detectados entre todos los que corresponden realmente a este.

¿Te parece un poco embrolloso?, lo resumiremos de esta forma:

• La precisión prioriza la minimización de los falsos positivos. Si necesitas que estos sean menores, utiliza esta métrica para ajustar los parámetros de tu modelo. Un ejemplo típico de esto es el diagnóstico médico, ya que un falso positivo se puede traducir en predecir incorrectamente una enfermedad (el positivo indica que el paciente está enfermo, por lo tanto, un falso positivo es un paciente mal diagnosticado con una enfermedad que no tiene), por lo que minimizar falsos positivos evita tratamientos innecesarios.
• La sensibilidad minimiza los falsos negativos. Si la prioridad es que el modelo no de por alto estos casos, esta métrica es la indicada para realizar ajustes. Un ejemplo de esto es la detección de fraudes, donde un valor negativo indica que una transacción no es un fraude; imagina que el modelo predice de forma errónea que una transacción fraudulenta no es un fraude, esto implicaría pérdidas monetarias.

Ahora mucho más resumido:

La importancia de la precisión o sensibilidad depende del contexto:

• Priorizar precisión: Si es crucial minimizar los falsos positivos.
• Priorizar recall: Si es crucial minimizar los falsos negativos.

Puntuación F1 (F1 Score)

Por último, el puntaje F1 es una métrica que combina la precisión y el recall en un único valor que equilibra ambas métricas. Es especialmente útil cuando se desea un balance entre precisión y recall.

 \text{F1} = 2 \times \frac{\text{Precisión} \times \text{Exhaustividad}}{\text{Precisión} + \text{Exhaustividad}}
 \tag{3.75}

Interpretación del puntaje F1

Los resultados de F1 se interpretan de la siguiente manera:

• F1 alto (valores cercanos a 1): Indica que el modelo tiene un buen equilibrio entre precisión y sensibilidad (recall). Es decir, detecta correctamente la mayoría de los positivos reales (alta sensibilidad) y sus predicciones positivas son confiables (alta precisión).
• F1 bajo (valores cercanos a 0): Refleja un desempeño pobre del modelo, ya sea porque tiene baja precisión (muchos falsos positivos), baja sensibilidad (muchos falsos negativos), o ambos.

El F1-Score es especialmente útil en escenarios donde:

• Hay un desequilibrio en las clases (una clase es mucho más frecuente que otra).
• Es importante un balance entre precisión y recall.
• Los falsos positivos y falsos negativos tienen un costo similar, y no se puede priorizar una métrica sobre la otra.

F1 es un mediador entre sensibilidad y precisión.

Cálculo e interpretación en el ejemplo propuesto

Calcularemos el puntaje F1 del modelo clasificador de reseñas:

\begin{aligned}
F1 &= 2 \cdot \frac{\text{Precisión} \cdot \text{Recall}}{\text{Precisión} + \text{Recall}} \\
   &= 2 \cdot \frac{0.8181 \cdot 0.9}{0.8181 + 0.9} \\
   &= 2 \cdot \frac{0.7363}{1.7181} \\
   &= 2 \cdot 0.4286 \\
   &= 0.8571
\end{aligned}

El F1-Score obtenido es de aproximadamente 0.85, lo que indica que el modelo tiene un buen equilibrio entre precisión (0.81) y recall (0.90). Esto significa que:

• Aunque hay algunos falsos positivos, la mayoría de las predicciones positivas son correctas (precisión moderadamente alta).
• El modelo es capaz de identificar correctamente una gran cantidad de reseñas positivas (recall/sensibilidad alta).

Nota sobre las métricas de la matriz de confusión

Las métricas antes expuestas, derivadas de la matriz de confusión, son muy variadas, pero la mayoría son poco conocidas. Esto es porque solo se suelen utilizar las que mencioné en la última lista. Sin embargo, como seguro ya saben, para mí es importante que tengan el conocimiento de todo el abanico de posibilidades que tienen a su disposición para evaluar modelos.

Una buena síntesis gráfica de estas medidas es la que se muestra en la Figura 3.7.5, donde se puede observar la relación que existe entre las métricas y los valores predichos y reales.

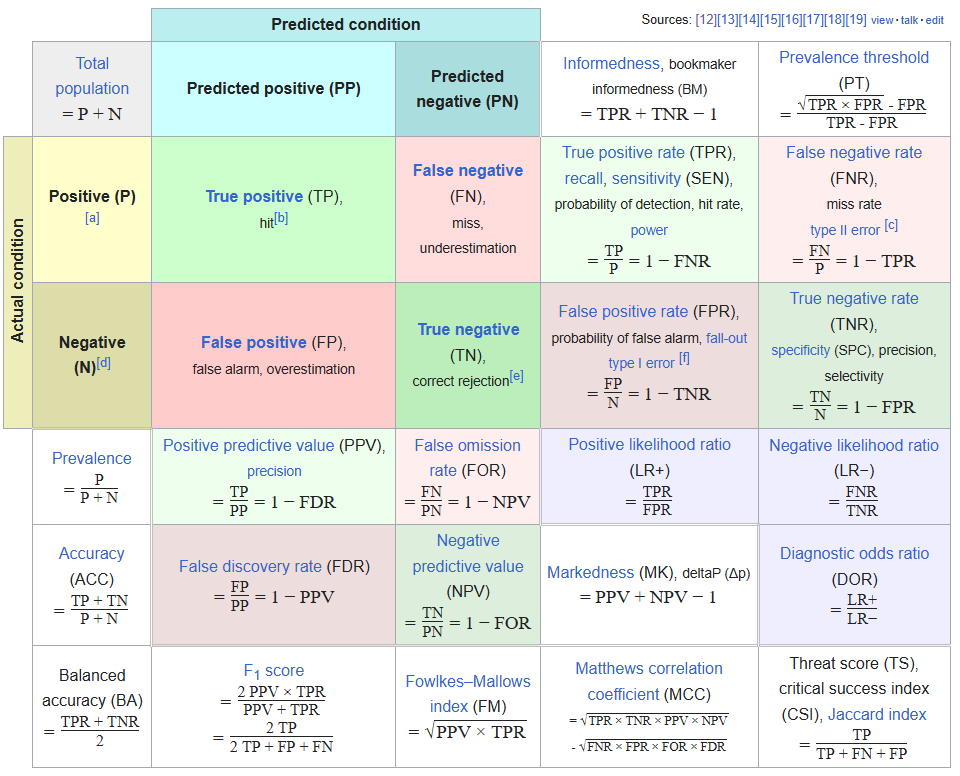
Esta imagen está en inglés porque proviene de Wikipedia en inglés, y la traducción automática al español me pareció imprecisa. Creo que tiene una organización que vale la pena revisar.

Que en este caso, son estas:

1.  Fawcett, Tom (2006). «An Introduction to ROC Analysis» (PDF). Pattern Recognition Letters. 27 (8): 861–874. doi:10.1016/j.patrec.2005.10.010. S2CID 2027090.
2. Provost, Foster; Tom Fawcett (2013-08-01). «Data Science for Business: What You Need to Know about Data Mining and Data-Analytic Thinking». O’Reilly Media, Inc.
3. Powers, David M. W. (2011). «Evaluation: From Precision, Recall and F-Measure to ROC, Informedness, Markedness & Correlation». Journal of Machine Learning Technologies. 2 (1): 37–63.
4. Ting, Kai Ming (2011). Sammut, Claude; Webb, Geoffrey I. (eds.). Encyclopedia of machine learning. Springer. doi:10.1007/978-0-387-30164-8. ISBN 978-0-387-30164-8.
5. Brooks, Harold; Brown, Barb; Ebert, Beth; Ferro, Chris; Jolliffe, Ian; Koh, Tieh-Yong; Roebber, Paul; Stephenson, David (2015-01-26). «WWRP/WGNE Joint Working Group on Forecast Verification Research». Collaboration for Australian Weather and Climate Research. World Meteorological Organisation. Retrieved 2019-07-17.
6. Chicco D, Jurman G (January 2020). «The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation». BMC Genomics. 21 (1): 6-1–6-13. doi:10.1186/s12864-019-6413-7. PMC 6941312. PMID 31898477.
7. Chicco D, Toetsch N, Jurman G (February 2021). «The Matthews correlation coefficient (MCC) is more reliable than balanced accuracy, bookmaker informedness, and markedness in two-class confusion matrix evaluation». BioData Mining. 14 (13): 13. doi:10.1186/s13040-021-00244-z. PMC 7863449. PMID 33541410.
8. Tharwat A. (August 2018). «Classification assessment methods». Applied Computing and Informatics. 17: 168–192. doi:10.1016/j.aci.2018.08.003.

En fin, solo estoy divagando de nuevo. Volvamos a donde estábamos.

Métricas de evaluación de modelos de clasificación con Python

Pasemos al campo de batalla. En esta práctica calcularemos medidas de evaluación de los modelos de clasificación que trabajamos en la introducción a la regresión logística, y haremos el análisis de los resultados, para derivar las conclusiones correspondientes.

Puedes previsualizar el contenido aquí:

Así concluye esta (un poco) larga sesión. Estas métricas las verás varias veces a lo largo de tu carrera, es por eso que le hemos dedicado especial detalle. En la siguiente aventura hablaremos sobre el subajuste y sobreajuste de modelos de machine learning, otro tópico altamente relevante para la ciencia de datos.