Entre los algoritmos de aprendizaje supervisado se pueden distinguir dos clases principales: de regresión y clasificación, siendo los de regresión aquellos que entregan salidas de tipo numéricas y continuas, mientras que los de clasificación producen valores discretos que fungen como clases para cada entrada. La regresión lineal aprendida en nuestra exploración anterior aborda los elementos y procesos matemáticos referentes al algoritmo de regresión más elemental del machine learning, y en esta ocasión nos toparemos con su hermana enfocada a la clasificación: la regresión logística.
La regresión logística se considera como uno de los componentes clave del aprendizaje de máquinas, principalmente para la creación de modelos de clasificación, y desde su estudio podemos no solamente comprender la esencia de su funcionamiento en cuanto a asignación de categorías, sino también conocer la percepción matemática del machine learning desde un enfoque probabilístico.
En esta excursión experimentaremos un viaje con emociones más tórridas: nos embarcaremos en la búsqueda y comprensión de este algoritmo desde una frívola descripción demostrativa hasta sus raíces matemáticas, y pondremos en práctica lo aprendido utilizando un conjunto de datos obtenido con la API de Spotify, lo cual nos permitirá operar sobre una minúscula muestra del big data generado por uno de los más icónicos gigantes tecnológicos de esta era.

Equipaje recomendado

Google Colab

Programación en Python

Preprocesamiento de datos

Matemáticas: principalmente álgebra, probabilidad y estadística.

Regresión lineal

Algún acompañamiento

Introducción a la regresión logística

El método de regresión lineal que hemos explorado anteriormente nos permite realizar estimaciones numéricas dado un conjunto de entradas (variables independientes) y una salida (variable dependiente) mediante la obtención de un modelo que describa la relación entre estas.
Este modelo, si bien es útil para realizar cálculos dadas variables continuas, no es de gran ayuda cuando es necesario asignar una categoría a un conjunto de entradas, es decir, ejecutar una tarea de clasificación.
Para esto es que se invoca a la regresión logística, un artefacto que utiliza principios de probabilidad para la categorización de datos, y el cual comenzaremos a sondear, al igual que hicimos con la regresión lineal, desde un ejemplo sobre su uso para la resolución de un problema.
Regresión logística: caso de uso
Para ejemplificar el empleo de la regresión logística, haremos uso de datos obtenidos de Spotify, la afamada plataforma de música vía streaming.
Supongamos que se nos ha asignado la tarea de crear un modelo capaz de clasificar una canción por su género dada su «bailabilidad» (danceability), la cual es una métrica (con un rango continuo de entre 0 y 1) creada por Spotify que determina qué tan adecuada es una canción para ser bailada; esto se define de acuerdo con la combinación de algunos elementos musicales como el tempo o la estabilidad del ritmo).

Justamente la idea de utilizar un modelo que aprenda a clasificar canciones utilizando esta métrica como atributo de entrada nos puede arrojar insights sobre si es una característica funcional o no.
El objetivo será clasificar un conjunto de canciones en dos géneros musicales respecto a su bailabilidad:
- Black metal.
- Reggaeton.
Para esto utilizaremos la regresión logística, y la forma en que atacaremos este problema es considerándolo desde un punto de vista probabilístico. La pregunta que intentaremos resolver sobre cualquier canción de nuestro conjunto de datos será la siguiente:
- Dado el grado de bailabilidad de una canción, ¿a qué género es más probable que pertenezca?
¿Qué es la regresión logística?
La regresión logística es un método matemático cuyo objetivo es modelar la probabilidad de que un evento pertenezca a una o más categorías dados los valores de una o más variables independientes.
Esto quiere decir, en el contexto de los algoritmos de clasificación, que el fin de la regresión logística es el de ajustar un modelo que pueda ser utilizado para calcular la probabilidad de que una entrada sea miembro de una clase en particular. La definición matemática de esto la veremos con más detalle en la siguiente sección.

Justo como se hace en una regresión lineal, la idea de obtener un modelo con la regresión logística es la de encontrar una ecuación que nos permita modelar la relación de las variables que determinan el comportamiento de los datos, y para ello el patrón a definir es el de una curva dibujada por una función llamada función logística.
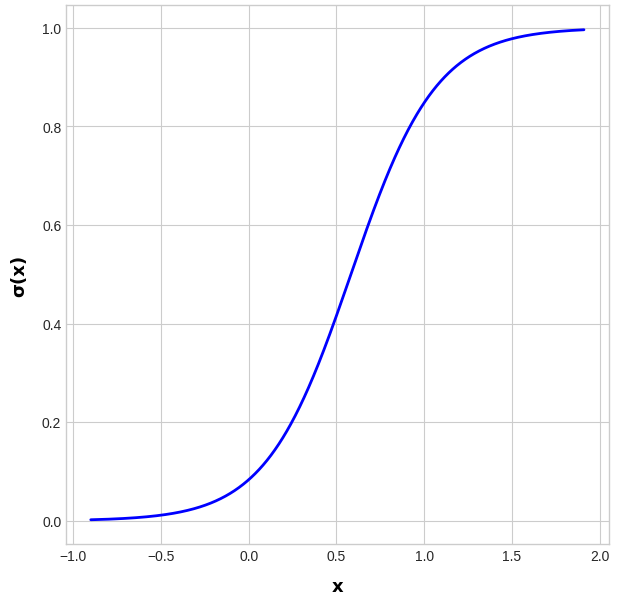
Como podrás notar en la Figura 3.3.1, la función logística (o función sigmoidea) genera una curva cuyos puntos se encuentran entre los valores 0 y 1 del eje vertical y. Esto quiere decir que cualquier entrada para el modelo será mapeada a un valor en este rango.

Espero que lo hayas vislumbrado. El transformar cada entrada en un número comprendido entre el 0 y el 1 es traducible a que la salida del modelo es una probabilidad. Recordemos que, dados los axiomas de Kolmogórov, todo valor de probabilidad está situado en este rango, siendo 1 la máxima probabilidad de que un evento suceda, y 0 la mínima.
Entre otras palabras, el modelo generado por la regresión logística tomará como entrada los datos a los que deseamos asignar una clase, y nos dará como salida la probabilidad de que estos pertenezcan a alguna categoría en particular, lo cual nos permitirá clasificarlos, como se ilustra en la Figura 3.3.2:
Asignación de clases
Ahora que hemos explorado algunos fundamentos de este método para realizar clasificaciones de datos, volvamos al caso planteado.
Echemos un vistazo a parte del conjunto de datos de canciones que vamos a utilizar:
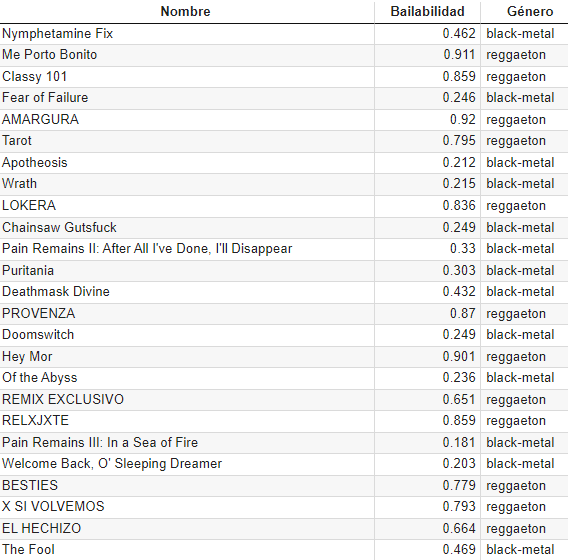
En la tabla se puede apreciar el nombre de la canción, su grado de bailabilidad, y el género al que pertenece. Estos datos etiquetados (con entradas y salidas definidas, justo como lo demandan los algoritmos de aprendizaje supervisado) serán procesados por la regresión logística, produciendo un modelo que nos ayudará a clasificar canciones nuevas.
Supongamos que ya hemos entrenado el modelo con estos datos, por lo que ahora lo probaremos con cinco canciones:
- Efecto
- Deathcrush
- Blow your trumpets Gabriel.
- TQG.
- Silver Lining.
Lo que haremos será evaluar cada una de estas con el modelo resultante, de forma que buscamos obtener la siguiente probabilidad:
p(canción pertenece a la clase black metal | bailabilidad)
Lo cual significa: probabilidad de que la canción pertenezca a la clase black metal dada su bailabilidad.
La probabilidad calculada por el modelo para cada canción se muestra en la siguiente tabla:
| Canción | Probabilidad |
|---|---|
| Efecto | 0.30 |
| Deathcrush | 0.83 |
| Blow your trumpets Gabriel. | 0.85 |
| TQG | 0.37 |
| Silver Lining | 0.77 |
De acuerdo con estas probabilidades, queda delegar cada canción a una clase. ¿Cómo se define esto?, esto se hace respecto a un umbral conocido como límite de decisión, el cual es el valor que define la probabilidad mínima necesaria para asignar un elemento a una clase específica. Sin ahondar en su cálculo por el momento, especificaremos que el límite de decisión para nuestro modelo es de 0.58, lo que significa que toda canción con una probabilidad mayor a este será considerada como parte de la categoría black metal.
El primer renglón, por ejemplo, nos dice que la probabilidad de que la canción Efecto sea del género del black metal es del 30%; al estar por debajo del umbral, se determina que esta no pertenece a esta categoría. Ahora, dadas las probabilidades, asignamos una clase a las 5 canciones:
| Canción | Probabilidad | Categoría asignada |
| Efecto | 0.30 | Reggaeton |
| Deathcrush | 0.83 | Black metal |
| Blow your trumpets Gabriel. | 0.85 | Black metal |
| TQG | 0.37 | Reggaeton |
| Silver Lining | 0.77 | Black metal |
En los algoritmos de clasificación procreados desde Python no es necesario realizar este último paso manualmente, todas las asignaciones de cada nueva observación se hacen de forma automática, junto con el ajuste del modelo.

Correcto, es una descripción básica, pero permite identificar los casos de uso de la regresión logística para modelos de clasificación.
Ahora que hemos explorado superficialmente este algoritmo de aprendizaje supervisado, podemos pasar a conocerla con mayor escrutinio, desde su anatomía matemática.
Matemáticas de la regresión logística

Para enunciar las definiciones matemáticas correspondientes para la comprensión de la regresión logística, atenderemos al ejemplo propuesto y el cómo resolverlo considerando lo que sabemos hasta ahora, de forma que alcancemos poco a poco tales definiciones.
Regresión lineal vs regresión logística para algoritmos de clasificación
Volvamos de nuevo al punto de inicio de nuestra tarea de clasificación de canciones, y realicemos una pregunta más específica:
- ¿Cómo puedo crear un algoritmo que clasifique canciones en dos categorías (reggaeton y black metal) dado su grado de bailabilidad?
Ahora intentaremos utilizar el conocimiento que ya tenemos de machine learning hasta nuestra exploración pasada para dar respuesta a esta cuestión, por lo que planteamos la siguiente pregunta:
- ¿Puedo utilizar una regresión lineal para obtener un modelo que haga los cálculos necesarios para este algoritmo de clasificación?
Al principio podría sonar relativamente confuso, o incluso sin sentido, ya que nuestra definición de regresión lineal no comprende el uso de probabilidades; sin embargo, podríamos pensar de manera no premeditada que es posible calcular la probabilidad p(x) como salida dados los valores de la variable independiente x. Es decir, postular p(x) como una función lineal de x como sigue:
\begin{aligned}
p(x)=\theta_{0}+\theta_{1}x\:. \tag{3.23}
\end{aligned}
Dicho esto, y con lo que ya se ha mencionado durante el recorrido, ¿puedes decir cuál es el mayor impedimento para que pueda modelarse de esta manera?

¿Lo recuerdas?, de nuevo se trata del rango en el que deben estar contenidas las salidas si estas son probabilidades. Recordemos que para toda probabilidad p(x) se cumple que p(x)\in(0,1), y las funciones lineales no están limitadas a estos valores, sus salidas pueden generar cifras tanto mayores a 1, como negativas.
Esta y otras razones no postulan a la regresión lineal como una buena candidata para el mapeo de probabilidades, y para algoritmos de clasificación en general.
Sin embargo, es conveniente encontrar una expresión lineal que pueda ser utilizada para modelar la relación entre las variables dependientes y la variable independiente, ya que permitiría entender cómo los cambios en las variables independientes afectan a la probabilidad de que ocurra un evento específico, el cual está representado por la variable dependiente. Por ello, buscaremos la forma de modelar la interacción lineal entre estas, y a su vez mapear sus salidas a una probabilidad.
Un elemento oportuno para esto es la razón de probabilidad (odds), la cual se escribe como sigue:
\begin{aligned}
\text{odds}=\frac{p(x)}{1-p(x)}\:, \tag{3.24}
\end{aligned}donde p(x) es la probabilidad de que ocurra un evento. Esta razón de probabilidades expresa la proporción o razón de la probabilidad de que ocurra un evento y la probabilidad de que no ocurra, y la utilizaremos para modelar las relaciones entre las variables que determinan esas ocurrencias o no ocurrencias.
Se asume, entonces, que esta razón de probabilidad puede ser expresada como una combinación lineal de las variables independientes (predictoras), es decir:
\begin{aligned}
\frac{p(x)}{1-p(x)}=\theta_{0}+\theta_{1}x\:. \tag{3.25}
\end{aligned}Ahora tenemos una ecuación que iguala la razón de las probabilidades de ocurrencia y no ocurrencia de un evento con la combinación lineal de las variables predictoras, permitiendo relacionar las probabilidades con los elementos de una expresión lineal. Sin embargo, hay una inconsistencia matemática relacionada a los valores que puede tomar la expresión lineal del lado derecho (su rango o imagen), los cuales se encuentran en el rango (-\infty,\infty), mientras que el rango de la función odds es (0,\infty). Para lidiar con esto, se realiza una transformación sobre la razón de probabilidades odds aplicando un logaritmo natural, quedando
\begin{aligned}
\mathrm{ln}(\frac{p(x)}{1-p(x)})=\theta_{0}+\theta_{1}x\:. \tag{3.26}
\end{aligned}Esta forma es llamada logit, y es conveniente en este sentido ya que la concordancia entre los rangos de ambos lados de la ecuación permiten la igualación de una combinación lineal de las variables independientes a la razón de probabilidades (ya que el rango de un logaritmo natural también es (-\infty,\infty)).
Finalmente, como buscamos obtener una función de probabilidad, despejamos p(x) en la ecuación, obteniendo
\begin{aligned}
p(y|x,\theta)=\frac{1}{1+e^{-(\theta_{0}+\theta_{1}x)}}\:. \tag{3.27}
\end{aligned}donde p(y|x,\theta) es equivalente a p(x), detallando que se expresa la probabilidad de que el evento y suceda dada la variable independiente x parametrizada por coeficientes \theta.
Esta forma final es conocida como función logística \sigma(x), y su principal virtud es que los valores que pueden tomar sus salidas oscilan entre el 0 y el 1, por lo que pueden ser interpretadas como probabilidades. En este caso, p(y|x;\theta) quiere decir «la probabilidad de y dados x y \theta. El rango de esta función es fácilmente constatable en la Figura 3.3.1:


Podemos resumir la lógica de lo que hemos revisado hasta ahora como sigue:
- Podemos tener la necesidad de modelar probabilidades condicionales para realizar clasificaciones de datos, pero la regresión lineal convencional no funciona adecuadamente para ello.
- Sin embargo, pretendemos utilizar un proceso de regresión asumiendo que la relación entre las variables inmiscuidas es lineal, por lo que igualamos el logaritmo natural de la razón de probabilidad a una combinación lineal de las variables predictoras o regresoras.
- Finalmente, se manipula la ecuación para definir la probabilidad en función de x y \theta, dando como resultado una función logística, la cual arroja salidas únicamente comprendidas entre 0 y 1, y que pueden ser interpretadas como probabilidades.
Con esto ya contamos con todos los elementos necesarios para hacer la definición formal de la regresión logística, la cual generalizaremos a más de una variable independiente.
Definición de la regresión logística
Definición 3.6 (Regresión logística). Dado un conjunto \lbrace (x_{1},y_{1}),…,(x_{N},y_{N})\rbrace de N observaciones o datos etiquetados, donde cada entrada x_n está compuesta por un conjunto \lbrace x_n^1, x_n^2, \ldots, x_n^D \rbrace de D variables independientes, predictoras o regresoras parametrizadas por un conjunto \lbrace\theta_0, \theta_1, \ldots, \theta_D\rbrace de D coeficientes correspondientes a cada variable regresora x_n^d , y cada salida del conjunto de datos es binaria, es decir, y_n \in {0, 1} , la regresión logística es un método que pretende modelar las relaciones entre estas entradas y salidas, y mapearlas a probabilidades mediante el ajuste de los parámetros de la función
\begin{aligned}
\sigma(x_n) &=p(y_{n}=1|x_{n},\theta)\\
&=\frac{1}{1+e^{-(\theta_0{} + \sum_{i=1}^D \theta_{d} x_n^{d})}}\:, \tag{3.28}
\end{aligned}donde p(y_n = 1|x_n, \theta) quiere decir <<probabilidad condicional de y_n = 1 dados los valores de la variable independiente parametrizada por \theta >>, donde 1 representa a una clase en particular. Es decir, p(y_n = 1|x_n, \theta) se refiere a la probabilidad de que una entrada x_n parametrizada por \theta pertenezca a una categoría arbitraria representada por el número 1.
Y en general, hay que tomar en cuenta que \sigma:\mathbb{R}\rightarrow(0,1).
Por último, tengamos en mente que la función sigmoidea de una sola variable, que es la que estaremos utilizando en nuestros ejercicios, tiene la siguiente forma:
\begin{aligned}
\sigma(x_n)=\frac{1}{1+e^{-(\theta_{0}+\theta_{1}x_n)}}\:, \tag{3.29}
\end{aligned}donde, recordemos, \sigma(x_n)=p(y_{n}=1|x_{n},\theta).

Veremos esta función aplicada a nuestro ejemplo, y su comprensión será mucho más fácil. Por lo pronto, hemos definido cómo es que la regresión logística mapea números reales a probabilidades condicionales, las cuales utilizamos para designar una entrada a una categoría específica. Antes de aplicar esto a nuestro ejemplo, veamos cómo estimar los parámetros de nuestra función, lo cual es el proceso de entrenamiento del algoritmo de machine learning.
Estimación de parámetros en la regresión logística
Existen varios métodos para ajustar los parámetros de un modelo de regresión logística, pero aquí haremos hincapié en uno en específico por el enorme eco que hace en la teoría del machine learning desde su perspectiva probabilística. Esta técnica es conocida como estimación de la máxima verosimilitud.
Estimación de la máxima verosimilitud (MLE)
La estimación de la máxima verosimilitud (MLE, por las siglas en inglés de Maximum Likelihood Estimation) es una metodología para estimar los parámetros de un modelo probabilístico mediante lo que se conoce como verosimilitud, el cual es un componente clave de la probabilidad bayesiana. En general, la MLE es comparable como marco general a la minimización del riesgo empírico.
Función de verosimilitud
Definición 3.7 (Función de verosimilitud). Dada una función de masa o función de densidad de probabilidad f(x|\theta), donde x_1, x_2, …, x_N son N observaciones independientes e identicamente distribuidas (iid), y \theta es el conjunto de parámetros \theta_1, \theta_2, …, \theta_D, la distribución de probabilidad conjunta de todas las observaciones es
\begin{aligned}
p(x_1, x_2,…, x_n|\theta)=f(x_1|\theta)f(x_2|\theta),...,f(x_n|\theta)\:. \tag{3.30}
\end{aligned}Esto es llamado función de verosimilitud, la cual expresa que los valores x_1, x_2, …, x_N son fijos, mientras que los parámetros \theta son variables, por lo que la función calcula las probabilidades de que dichas observaciones se den dados ciertos valores de los parámetros (es decir, qué tanto los valores de los parámetros generan a las observaciones).
Tomando en cuenta que las observaciones son independientes y que la probabilidad es conjunta, reescribimos la función de verosimilitud \mathcal{L}(\theta|x) como
\begin{aligned}
\mathcal{L}(\theta|x_1, x_2,…, x_n) = \prod_i^nf(x_i|\theta)\:. \tag{3.31}
\end{aligned}Esta función determina qué tanto los valores que parametrizan a una distribución de probabilidad generan a las observaciones del conjunto de datos, por lo que puede ser utilizada para encontrar dichos valores.
Nótese que la notación cambia ligeramente para expresar que ahora los datos observados x_1, x_2,…, x_n son fijos, y los parámetros \theta son las incógnitas o las variables que queremos ajustar. Por lo tanto, se reorganiza el enfoque de la notación para resaltar que la función depende de \theta, mientras que los datos son un componente fijo.
Definición 3.8 (Estimación de la máxima verosimilitud). Dada la función de verosimilitud mostrada en (3.31), el método de estimación de máxima verosimilitud \hat{\theta} consiste en maximizar la probabilidad de obtener las salidas del conjunto de datos dados los valores de los parámetros mediante la operación
\begin{aligned}
\hat{\theta}=\mathrm{arg\:max}\mathcal{L}(\theta|x_1, x_2,…, x_n)\:, \tag{3.32}
\end{aligned}lo cual quiere decir que, al maximizar la probabilidad de que tales parámetros produzcan las observaciones, se hace una estimación de los valores que parametrizan al modelo (la función de distribución de probabilidad).
Entre otras palabras, para un modelo probabilístico, la máxima verosimilitud puede ser utilizada para estimar los valores de sus parámetros, así como se utiliza la minimización del riesgo empírico en algoritmos como la regresión lineal.
Máxima verosimilitud en la regresión logística
No ahondaremos mucho en todo el proceso matemático involucrado en la estimación de los parámetros de la regresión logística utilizando la máxima verosimilitud, pero sí hablaremos un poco sobre las consideraciones matemáticas que conducen al cómo realizarla.
Debemos recordar que el objetivo del modelo obtenido por la regresión logística es predecir la probabilidad de ocurrencia de un evento binario en función de un conjunto de variables predictoras, por lo que la distribución de probabilidad que mejor se adecúa a este caso es la distribución de Bernoulli:
\begin{aligned}
f(x;p) = p^x(1-p)^{1-x}, \quad x \in {0,1}\ \tag{3.33}
\end{aligned}donde p es la probabilidad de éxito de un experimento, o probabilidad de que x=1, siendo x el resultado del experimento.
Sabiendo esto, tenemos que la función de verosimilitud de la distribución de Bernoulli que utilizaremos para estimar los parámetros es:
\begin{aligned}
\mathcal{L}(\theta) = \prod_{n=1}^{N} p_n^{y_n}(1-p_n)^{(1-y_n)}\:, \tag{3.34}
\end{aligned}donde p_n es la probabilidad de que y=1 dadas las variables predictoras x_n^{d} y los parámetros \theta, es decir,
\begin{aligned}
p_n = p(y = 1 | x_n, \theta) =\frac{1}{1+e^{-(\theta_0{} + \sum_{i=1}^D \theta_{d} x_n^{d})}}\:. \tag{3.35}
\end{aligned}Además, la función de verosimilitud se suele expresar en términos de un logaritmo natural para la simplificación de cálculos, dando como resultado que la estimación de parámetros del modelo esté dada por
\begin{aligned}
\mathrm{arg\:max}\:\mathcal{L}(\theta|x_1, x_2,…, x_N) = \sum_{n=1}^{N} y_n \log(p_n) + (1 - y_n) \log(1-p_n)\:, \tag{3.36}
\end{aligned}siendo esta la forma final de la función que ajusta los valores de los parámetros del modelo.


Aplicación de la regresión logística para clasificación de datos
Es tiempo de volver al ejemplo planteado y explicar cómo es que el modelo obtenido puede ser utilizado para realizar las clasificaciones deseadas.
Supongamos que hemos utilizado la regresión logística alimentando al algoritmo con nuestros datos de canciones, tomando ahora como objetivo a la clase «reggaeton» (ahora buscamos predecir qué tan probable es que una canción sea de reggaaeton según su bailabilidad), y el ajuste de los parámetros ha quedado como sigue:
\theta_{0} = -2.28
\theta_{1} = 4.12
Dado que solo tenemos una variable independiente, o regresor, el cual es la bailabilidad de la canción, utilizamos el modelo de regresión logística univariable mostrada en la Ecuación (3.29), donde al sustituir con los valores de los parámetros obtenidos de la fase de entrenamiento, quedaría como sigue:
\begin{aligned}
\sigma(x_n)=\frac{1}{1+e^{-(-2.28+4.12(x_n))}} \tag{3.37}
\end{aligned}Ahora tomaremos dos canciones del conjunto de prueba y estimaremos la probabilidad de que pertenezcan a la categoría reggaeton, que está representada con el número 1. Las canciones a utilizar serán Deathmask Divine y Gasolina (un clásico de clásicos), cuyos grados de bailabilidad son:
| Canción | Bailabilidad |
| Deathmask Divine | 0.43 |
| Gasolina | 0.85 |
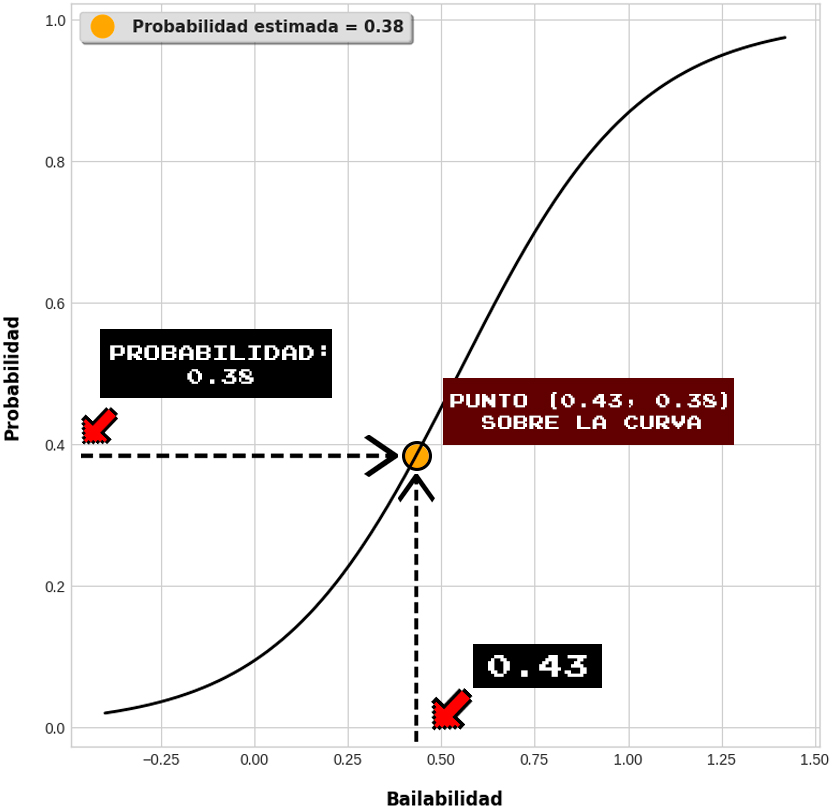
Realizamos el cálculo para la primer canción utilizando la función sigmoidea, donde x_n=0.43:
Estimación de probabilidad para Deathmask Divine
\begin{aligned}
\sigma(0.43)=\frac{1}{1+e^{-(-2.28+4.12(0.43))}}=0.38 \tag{3.38}
\end{aligned}Para entender cómo es que el patrón descrito por esta función dibuja las probabilidades en función de las entradas, observemos la gráfica de la estimación dada para Deathmask Divine:
Ahora realizamos el cálculo para la canción Gasolina, con x_n=0.85.
Estimación de probabilidad para Gasolina
\begin{aligned}
\sigma(0.85)=\frac{1}{1+e^{-(-2.28+4.12(0.85))}}=0.77 \tag{3.39}
\end{aligned}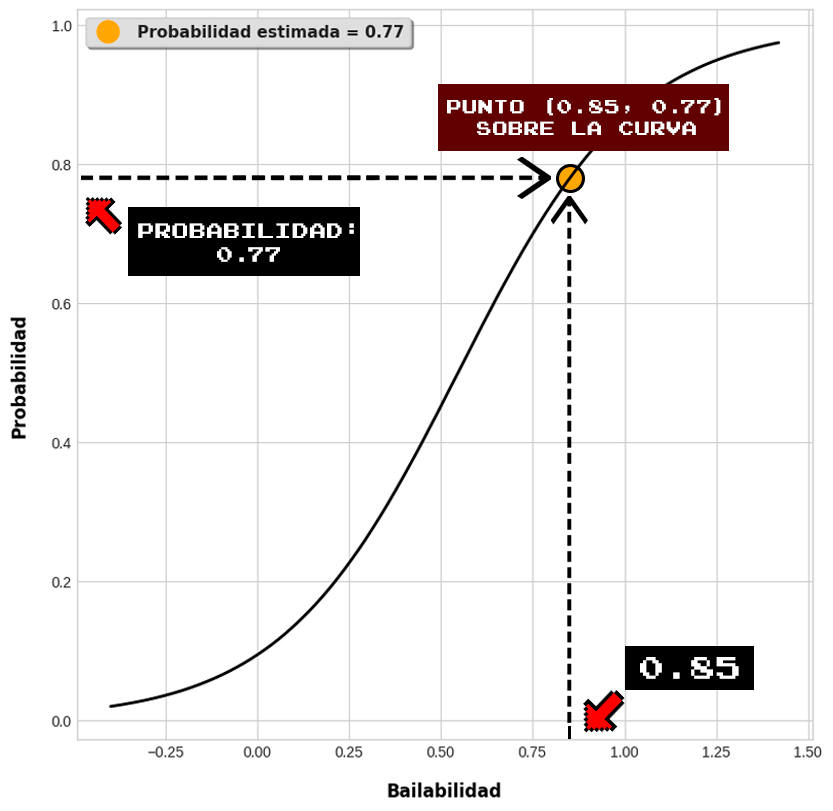
Se puede apreciar cómo las probabilidades son marcadamente diferentes para cada una, pero ¿cómo es que nuestro algoritmo de machine learning decidirá etiquetar nuestros datos en clases utilizando estos valores?
Este es el paso final, y la respuesta a esto es un elemento conocido como límite de decisión.
Límite de decisión
Para asignar categorías a cada dato dada la probabilidad mapeada por la función logística se utiliza el límite de decisión, el cual es el umbral que define si esta probabilidad es suficiente o insuficiente para que una observación pertenezca a la clase de referencia.
Definición 3.9 (Límite de decisión). Dada la función logística generada por la regresión logística, el límite de decisión b_{dec} se obtiene mediante
\begin{aligned}
b_{dec}=-\frac{\theta_{0}}{\theta_{1}}\:\, \tag{3.40}
\end{aligned}cuyo resultado es la frontera en la que la probabilidad de pertenecer a una clase es igual a 0.5, es decir, determina qué valor de las salidas de la función sigmoidea funge como el umbral entre la asignación de una clase u otra.
Para entenderlo mejor, procederemos a calcular el valor del límite de decisión para nuestro modelo:
\begin{aligned}
b_{dec}=-\frac{-2.39}{4.12}=0.58\:\, \tag{3.41}
\end{aligned}Por lo tanto, para toda canción con probabilidad p(y=1|x,\theta) estimada por la función logística, se cumple que:
- La canción pertenece a la clase 1 si su probabilidad es mayor a 0.58 (si p>b_{dec}).
- La canción pertenece a la clase 0 si su probabilidad es menor que 0.58 (si p<b_{dec}).
De acuerdo con esto, veamos qué categorías corresponden a cada una de las canciones seleccionadas a evaluar:
| Canción | Probabilidad | Categoría estimada |
| Efecto | 0.73 | Reggaeton |
| Deathcrush | 0.20 | Black metal |
| Blow your trumpets Gabriel | 0.17 | Black metal |
| TQG | 0.66 | Reggaeton |
| Apotheosis | 0.19 | Black metal |

Con esto queda entendido que este umbral nos dice si un dato pertenecerá o no a una clase: si la probabilidad calculada para cierta observación está por encima del límite, entonces pertenece a la clase de referencia, y viceversa.
De forma gráfica, el límite de decisión para una función sigmoidea con una variable predictora luce como una línea recta, la cual separa las observaciones después de haberse adjudicado a alguna clase:
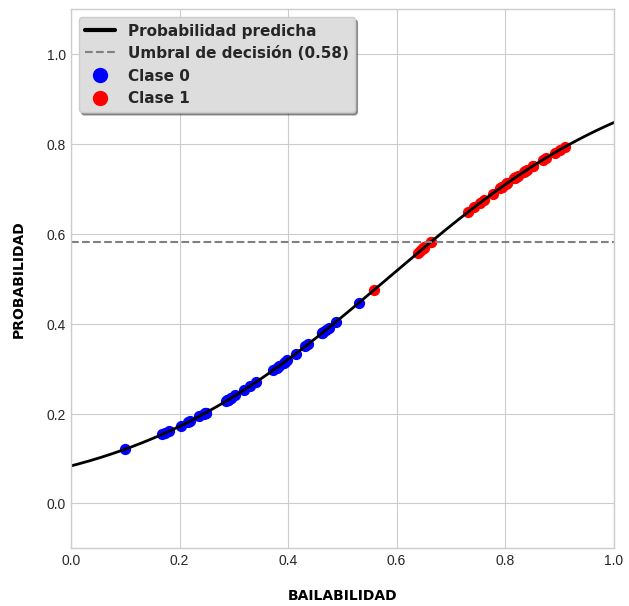
En la gráfica se puede notar que el modelo no es un predictor perfecto: existen algunos puntos debajo del umbral de decisión que aún forman parte de la clase objetivo, lo cual es normal sabiendo que se trata de un fenómeno no determinista.
Para concluir, con toda esta información, ¿puedes contestar a la pregunta planteada al inicio de la sección?
Pregunta:
- ¿Cómo puedo crear un algoritmo que clasifique canciones en dos categorías (reggaeton y black metal) dado su grado de bailabilidad?
La respuesta corta sería: modelando la relación que existe entre la bailabilidad y la probabilidad de que una canción pertenezca a una de las clases, mapeando el resultado a un rango de probabilidades utilizando un modelo ajustado por una regresión logística, la cual calculará los parámetros del modelo maximizando la verosimilitud de su distribución de probabilidad (de Bernoulli), dando como resultado una función que genera probabilidades respecto a una entrada parametrizada, y la cual puede ser utilizada para definir si una canción pertenece o no a una clase respecto a un umbral de decisión.

Es una buena pregunta, ya que es muy probable necesitar hacer clasificaciones con más de dos clases, la regresión logística de clases múltiples es un tema que retomaremos más adelante y abordaremos con mayor escrutinio. Por el momento, nos limitaremos a saber que sí es posible hacer esto, y que las técnicas más conocidas para ello son las siguientes:
- Uno contra el resto (One-vs-Rest).
- Softmax o Regresión Logística Multinomial.
De entre las cuales la función softmax será tema de discusión en una expedición próxima, ya que es un elemento recurrente en modelos de aprendizaje automático. La regresión multiclase la podrás experimentar en la práctica en Python de la siguiente sección.

Regresión logística: código de programación en python

Hora de aplicar lo aprendido a un conjunto de datos reales. En esta ocasión, como ya se ha hecho mención durante toda la expedición, utilizaremos un conjunto de datos generado haciendo uso de la API de Spotify. Si te interesa aprender a hacer esto, visita el tutorial en este link.
Por lo pronto, es momento de ponernos manos a la obra:

También puedes observar el código y previsualizar sus salidas en la siguiente ventana, pero sin posibilidad de ejecutarlo:
Ahora tenemos un conocimiento más que suficiente de lo que es, cómo, y para qué se utiliza la regresión logística. Este algoritmo es el que utilizaremos para introducir conceptos básicos de machine learning relativos a los algoritmos de clasificación, mientras que utilizaremos la regresión lineal para aquellos que arrojan estimaciones en rangos numéricos continuos. Estamos por comenzar a tantear terrenos que competen a fundamentos importantes del aprendizaje de máquinas, y que nos conducirán a uno de los modelos más consagrados de su historia: la red neuronal artificial.




Quiero que la IA lave los trastes y barra la casa mientras yo hago arte, no al revés.