Al momento de concluir la etapa de entrenamiento de un modelo de machine learning, uno de las tareas posteriores e imprescindibles es la evaluación de su desempeño. Al obtener estas medidas, es muy común encontrar que los modelos no son capaces de realizar inferencias correctamente sobre un conjunto de datos de prueba. Esta problemática generalmente se suele etiquetar en dos categorías principales: sobreajuste y subajuste de modelos.

Este par de situaciones son muy comunes a la hora de modelar datos mediante algoritmos de aprendizaje supervisado. Aquí exploraremos cada uno de estos, describiremos sus causas, consecuencias, diagnóstico, y abordaremos algunos ejemplos de forma teórica y práctica con lenguaje de programación Python.

Inventario recomendado

Regresión lineal

Métricas de evaluación de modelos de regresión

Google Colab

Programación en Python

Algún tentempié

Introducción al sobreajuste y subajuste de modelos de machine learning

Como ya hemos visto durante nuestras dos últimas prácticas para la evaluación de modelos de aprendizaje supervisado (tanto de regresión como de clasificación), existen diferentes formas de medir el desempeño de un modelo cuyos parámetros han sido ajustados mediante algoritmos de machine learning.

Durante la evaluación del modelo resultante, pueden develarse problemas al momento de realizar los cálculos sobre los conjuntos de datos de entrenamiento y prueba. Lo más común es encontrar que, si los modelos no realizan predicciones de manera relativamente aceptable, entonces están sobreajustados o subajustados. ¿A qué nos referimos con esto?

¿Qué es el subajuste de un modelo de machine learning?

Un modelo subajustado es un modelo de aprendizaje de máquinas que no logra capturar o «aprender» correctamente los patrones subyacentes a los datos debido, principalmente, a su simplicidad matemática (del modelo generado) y, por lo tanto, tiene un desempeño deficiente al ser evaluado tanto en el conjunto de datos de entrenamiento como en el de prueba.

Es correcto, sus capacidades predictivas no muestran un rendimiento aceptable al ser utilizado para predecir valores en los conjuntos de datos para su entrenamiento y prueba. Esta es su característica más distintiva.

Para entender mejor cómo funciona esta deficiencia en el ajuste del modelo (el cálculo de sus parámetros) es observando las gráficas de la Figura 3.8.1, donde se observan las formas que dibujan dos modelos que pretenden describir el comportamiento de los datos:

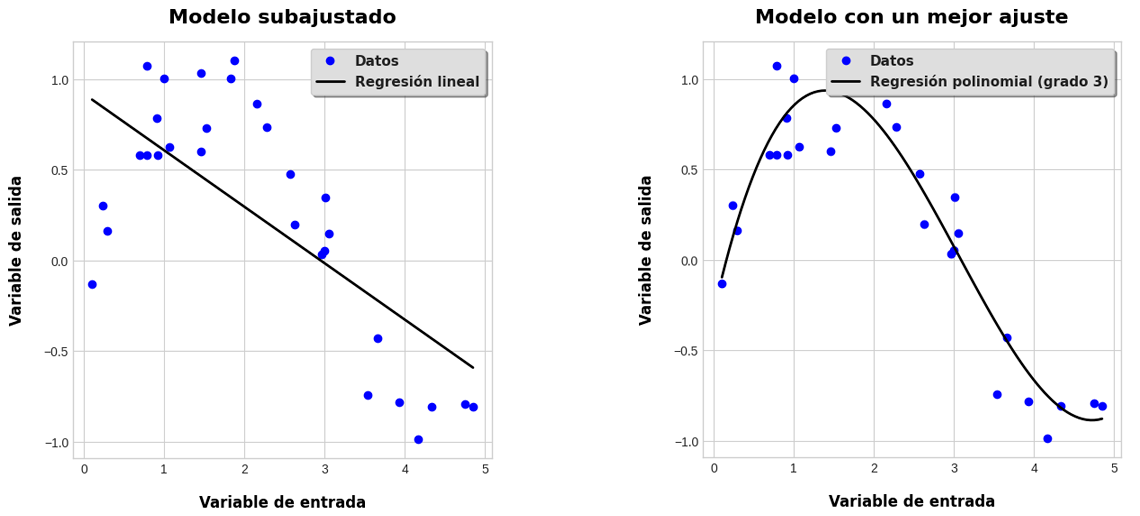
Nótese que la primera figura es una línea recta como la que hemos generado con las regresiones lineales de las prácticas anteriores. A pesar de que la función que dibuja esta línea está optimizada para mantener una distancia promedio corta respecto a cada punto (dato), esta no representa una tendencia muy similar a la que dibujan los datos (que parecen dibujar una especie de curva). Se dice, entonces, que el modelo está subajustado, ya que sus predicciones no son muy precisas al momento de evaluar su desempeño.

En cambio, en la gráfica de la derecha, se han mapeado los valores de una función que genera una forma más ajustada al movimiento de los datos. Esta curva se puede obtener utilizando regresiones polinomiales. El modelo resultante tiene un mejor desempeño en las predicciones.

Una regresión polinomial es una regresión lineal que modela un polinomio de n-ésimo grado. No la utilizaremos mucho, por lo que no ahondaremos en el tema, si deseas saber más puedes revisar la definición en Wikipedia, la cual me ha parecido correcta y concisa, pero no es necesario que lo atiendas. También utilizaremos esto más tarde en nuestra práctica de Python.

Matemáticamente hablando, los modelos de ambos ejemplos (Figura 3.8.1) tienen la siguiente forma:

• Modelo subajustado (regresión lineal):

y = ax + b \tag{3.76}

• Modelo con un mejor ajuste (regresión polinomial de grado 3):

y = ax^3 + bx^2 + cx + d  \tag{3.77}

Hago este énfasis porque la elección del algoritmo utilizado para entrenar el modelo muchas veces es un aspecto clave para un ajuste efectivo de los parámetros. Nótese que los modelos presentados son solo la forma general de estos, donde los valores de los parámetros (a, b, c, d...) son los que se encuentran mediante la etapa de entrenamiento con un algoritmo de aprendizaje supervisado.

Finalmente, hay que tomar en cuenta que las deficiencias características del subajuste se encuentran directamente al medir el rendimiento del modelo en los conjuntos de datos de entrenamiento y prueba; esto es lo que hicimos durante nuestras últimas dos prácticas, en especial en la que corresponde a las métricas de evaluación de modelos de regresión (ya que acabamos de plantear el uso de regresiones lineales).

Hagamos un pequeño ejercicio al respecto, para refrescar nuestra memoria en el tema:

Esto quedará mucho más claro en nuestra práctica con Python, donde veremos ejemplos que analizaremos con métricas de evaluación.

Posibles causas de un modelo subajustado

Las razones por las que un modelo puede sufrir un subajuste pueden ser variadas y depender de los datos y el tipo de algoritmo utilizado para ajustar los parámetros. Sin embargo, estas pueden ser las causas más comunes para un subajuste:

• Modelo demasiado simple: No tiene suficiente capacidad para aprender patrones complejos. Esto se vio en el ejemplo de la Figura 3.8.1, donde un modelo como el que produce una regresión lineal simple (univariada) no es lo mejor en datos con patrones no lineales.
• Falta de datos: No hay suficiente información para aprender relaciones significativas entre las variables de entrada y las salidas, es decir, se requiere de un conjunto de datos más grande.
• Muy pocas características: No se han incluido variables de entrada clave en los datos de entrenamiento. Por ejemplo, si se desea obtener un modelo que sea capaz de predecir la calificación que obtendrá un alumno en un examen, probablemente los datos que pueden aportar información al respecto son: horas de estudio, calificaciones promedio, o estatus social. En cambio, variables que no aportan información relevante pueden ser: nombre del alumno, día de nacimiento, rango en Fortnite, etc.
• Mala selección de hiperparámetros: existen algunos parámetros relativos a los algoritmos utilizados, que veremos más adelante en el curso, que pueden ser decisivos en el ajuste final del modelo, algunos ejemplos son: número de iteraciones, regularización, optimizador, tasa de aprendizaje.

¿Qué es el sobreajuste de un modelo de machine learning?

Un modelo sobreajustado es un modelo obtenido mediante algoritmos de aprendizaje de máquinas cuyo comportamiento se adhiere de manera muy fiel a la tendencia de los datos de entrenamiento, con un ajuste que no solo captura los patrones subyacentes, sino también el ruido y las variaciones irrelevantes.

Esto provoca que el modelo tenga un rendimiento muy aceptable al evaluarse en el conjunto de datos de entrenamiento, pero que sea deficiente al operar sobre datos nuevos (es decir, en el conjunto de datos de prueba, o datos nuevos recolectados), ya que no logra generalizar bien su comportamiento.

A diferencia del subajuste, el sobreajuste ocurre cuando el modelo es demasiado complejo en comparación con la estructura de los datos. Como mencionó Mmerf, en la etapa de entrenamiento su desempeño luce muy bien, pero al evaluarse con los datos de prueba ya no funciona de igual manera.

El efecto del sobreajuste se observa en las gráficas de la Figura 3.8.2:

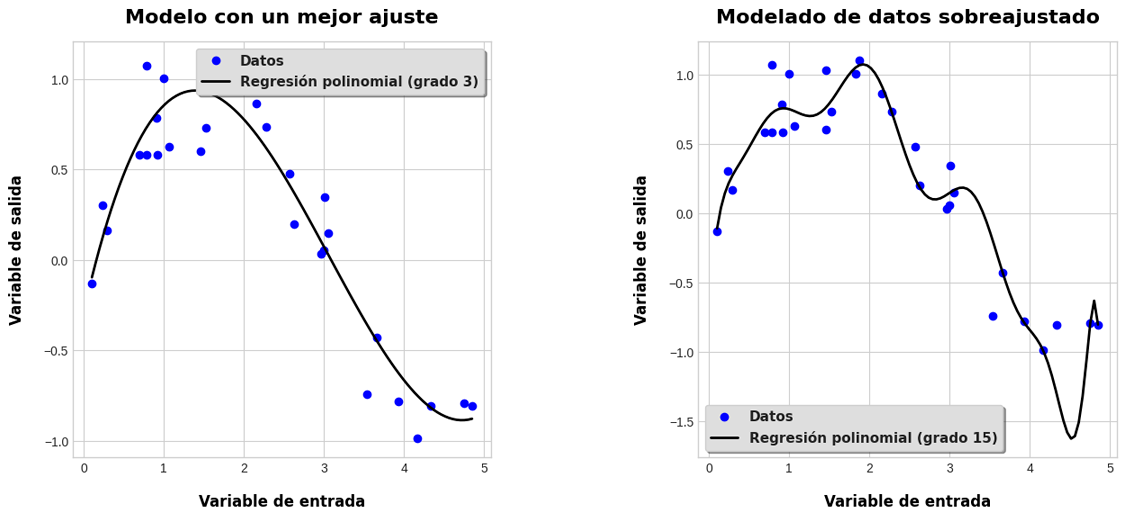
En este caso, en la primera gráfica yace el modelo que vimos anteriormente, donde los datos pueden ser modelados mediante una curva que decae sutilmente y se ajusta a su comportamiento sin encajar perfectamente en estos, lo que implica que realiza predicciones con pequeños defectos pero cercanas a la tendencia subyacente.

En la figura de la derecha, sin embargo, se visualiza una función que está demasiado ajustada al movimiento de los datos, provocando que se dibuje una figura irregular que intenta abarcar las variaciones de todas las observaciones, aunque estas puedan representar valores atípicos o ruido; obsérvese el último punto, el cual parece ser un valor atípico en el conjunto de datos, y que el modelo traza de manera exacta.

Esto implica que el modelo está sobreajustado, generando una función matemática que predice correctamente solo los valores del conjunto de datos de entrenamiento, pero falla en el conjunto de datos de prueba (no es capaz de realizar estimaciones correctas sobre valores cuya tendencia en realidad es una curva, no un conjunto de valles irregulares, como lo que se ha dibujado en la gráfica de la derecha).

Matemáticamente hablando, los modelos de ambos ejemplos tienen la siguiente forma:

• Modelo con un mejor ajuste (regresión polinomial de grado 3):

y = ax^3 + bx^2 + cx + d

• Modelo sobreajustado (regresión polinomial de grado 15):

y = a_{15}x^{15} + a_{14}x^{14} + \dots + a_2x^2 + a_1x + a_0

De esto se desprende que utilizar modelos de varias dimensiones (variables) y grados altos puede desembocar en un sobreajuste, por lo que es necesario tener cuidado en mantener un balance entre los algoritmos de aprendizaje de máquinas a utilizar y las dimensiones de entrada de los datos.

Las gráficas finales de cada modelo con ajustes diferentes se pueden contemplar en la Figura 3.8.3

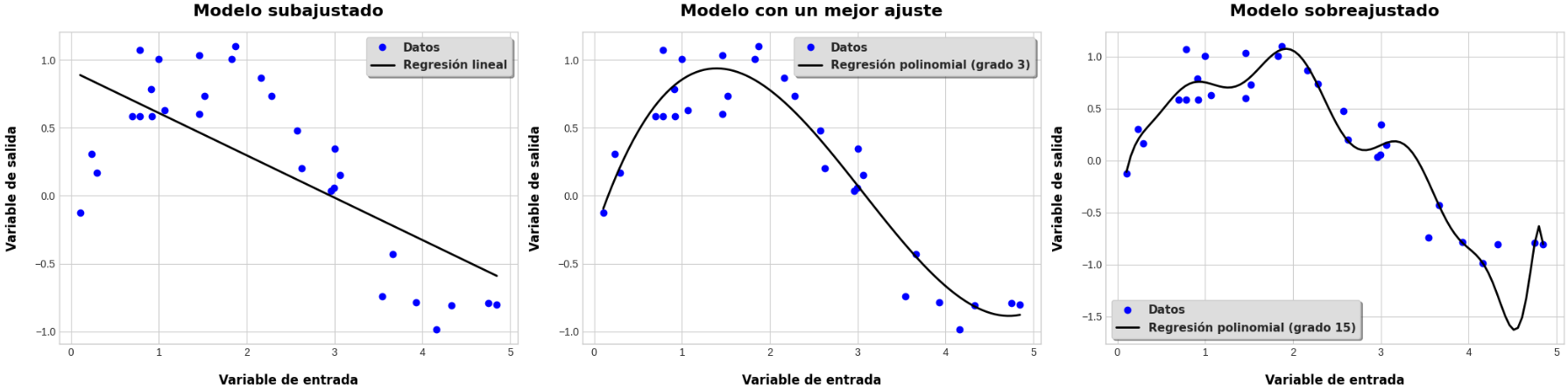
Así es, los modelos de clasificación pueden tener los mismos problemas. Para identificarlos se sigue la misma metodología, se realizan las respectivas mediciones de desempeño utilizando métricas de evaluación de modelos de clasificación.

Posibles causas de un modelo sobreajustado

Las razones por las que un modelo puede sufrir sobreajuste, al igual que en el subajuste, pueden ser variadas y dependen principalmente del conjunto de datos y/o de la complejidad del modelo utilizado. A continuación, se presentan algunas de las causas más comunes para un sobreajuste:

• Modelo demasiado complejo: Tiene una gran cantidad de parámetros y variables, lo que le permite aprender incluso el ruido en los datos en lugar de los patrones generales.
• Demasiadas características irrelevantes: Si el modelo tiene muchas variables que no aportan información útil, puede ajustarse demasiado a datos específicos sin realizar generalizaciones correctamente.
• Insuficiente cantidad de datos: Con pocos datos, el modelo puede aprender patrones específicos del conjunto de entrenamiento en lugar de patrones generales.
• Las particiones del conjunto de datos no tienen la misma distribución: Los conjuntos de datos de entrenamiento prueba y/o validación no muestran consistencia en su comportamiento.
• Mala selección de hiperparámetros: Algunos parámetros, como la falta de regularización o arquitectura del algoritmo a utilizar, pueden hacer que el modelo sea demasiado flexible y se adapte al ruido.

Detección de ajuste y sobreajuste de modelos con Python

Es hora de un poco de acción. En la práctica de hoy revisaremos un caso de subajuste y sobreajuste de modelos, realizando diagnósticos con métricas de evaluación.

Puedes previsualizar el contenido aquí:

Hemos concluido uno de los temas más comunes de deficiencias en modelos de aprendizaje de máquinas. Conforme avancemos en esta travesía, experimentaremos formas de identificar y lidiar con estos desperfectos.

A partir de ahora, los temas serán un poco más avanzados y enfocados en la optimización del entrenamiento de modelos, ya que constituyen el preámbulo para la comprensión y práctica de las redes neuronales artificiales.